はじめに
擬フォークト分布関数(Pseudo-Voigt function)は、ガウス分布関数とローレンツ分布関数の線形結合として表される関数です。この関数は特にX線回折やスペクトル分析などで観測されるピークの形状を表現するのに適しています。
コード
解説
モジュールのインポート
バージョン
データの生成
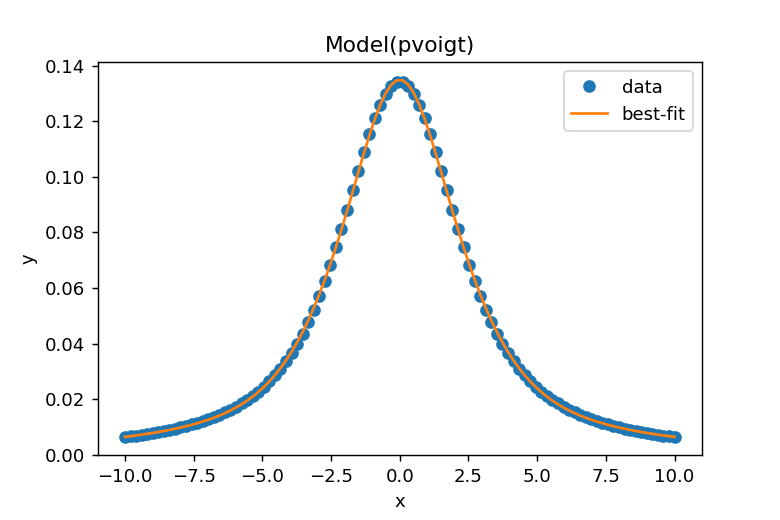
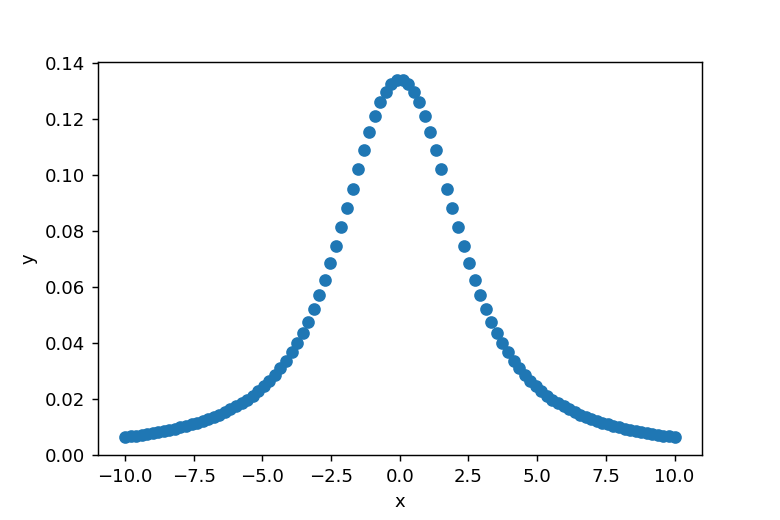
SciPyのspecial.voigt_profileを使用してフォークト分布のラインプロファイルを作成できます。xとyの関係を図で示すと以下のようになります。
モデルの定義
lmfit.models モジュールの
PseudoVoigtModel をモデル関数として使用します。擬Voigt関数は特定の数式で表現され、そのパラメータには振幅(amplitude)、中心位置(center)、幅(sigma)、およびガウス成分とローレンツ成分の混合比率(α)が含まれます。
\[f(x; A, \mu, \sigma, \alpha) = \frac{(1-\alpha)A}{\sigma_g\sqrt{2\pi}}
e^{[{-{(x-\mu)^2}/{{2\sigma_g}^2}}]}
+ \frac{\alpha A}{\pi} \big[\frac{\sigma}{(x – \mu)^2 + \sigma^2}\big]\]
初期パタメータの推定
model.guess(y, x=x)により、上図のデータを擬フォークト関数モデルで近似するためのフィッティングパラメータについて、初期値を推定します。パラメータ(params)は以下のようになります。
カーブフィット
model.fit(y, params, x=x)により、カーブフィッティングを実行します。
フィッティング結果の表示
print(result.fit_report())により、フィッティングの結果を見ることができます。
result.plot_fit()によりデータとフィッティングカーブが表示されます。

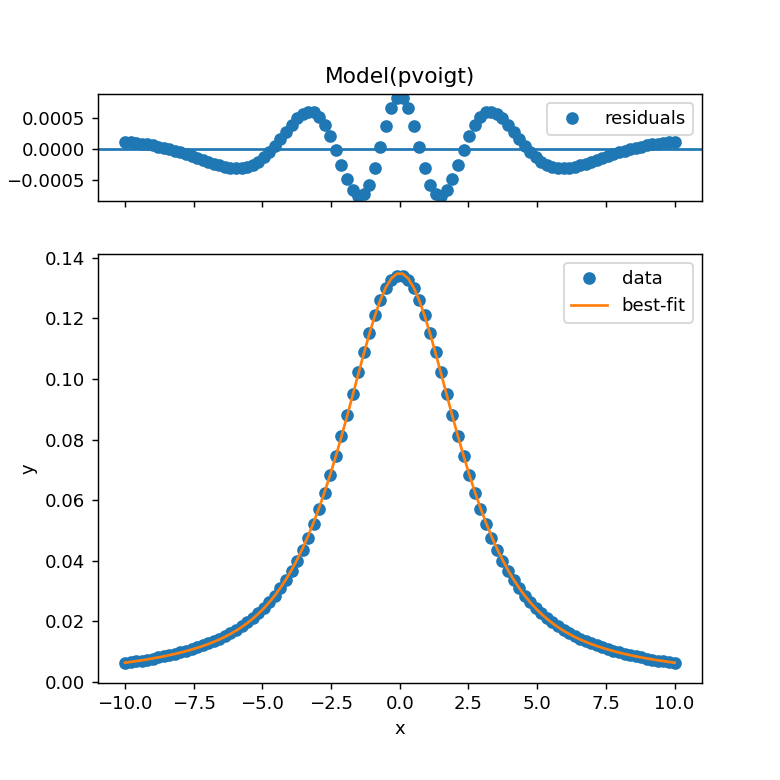
result.plot()とすることで残差とともにフィッティング結果が表示されます。
まとめ
擬フォークト分布関数は、スペクトル解析や回折パターン解析において非常に有用なツールです。lmfitライブラリを使用することで、このような複雑な関数でも簡単にカーブフィッティングを行うことができます。パラメータに制約を設けることで、より物理的に意味のある結果を得ることも可能です。
特に、複数のピークを持つデータに対しても、モデルを組み合わせることで効果的なフィッティングが実現できます。これにより、スペクトルの重なりなど、実験データの複雑な特性も分析できるようになります。

コメント