はじめに
データ分析において、モデルフィッティングは単にパラメータを推定するだけでなく、そのモデルの予測がどの程度信頼できるかを評価することも重要です。この記事では、Pythonのlmfitライブラリを使用して、モデルの不確実性を定量化し、信頼区間と予測区間を計算・可視化する方法を解説します。
不確実性の種類: 信頼区間と予測区間
モデルの不確実性を考える上で、2つの重要な概念があります:
- 信頼区間 (Confidence Interval): モデルの平均応答に関する不確実性。つまり、「真の回帰線がこの範囲内にある確率は95%」という情報を与えます。
- 予測区間 (Prediction Interval): 個々の新しいデータポイントの予測に関する不確実性。信頼区間より広くなり、「新しいデータポイントがこの範囲内に入る確率は95%」という情報を提供します。
必要なライブラリ
モジュールのインポート
バージョン
サンプルデータの準備
このコードは具体的に:
- まず乱数のシード値を0に設定して再現性を確保
- x軸データとして0から10の範囲に100点を均等に配置
- 真の関数値y_trueを計算(ガウス関数と線形項の組み合わせ):
- ガウス関数: 振幅3.0、中心5.0、標準偏差2.0
- 線形項: 傾き0.1
- 最後に、平均0、標準偏差0.5のガウスノイズをy_trueに追加して観測データyを作成
モデルフィッティング
このコードは、lmfitライブラリを使用して合成モデル(ガウシアンモデル+線形モデル)を作成し、データにフィッティングする部分です。
- モデルの定義:
- ガウシアンモデル(
GaussianModel)と線形モデル(LinearModel)をそれぞれ作成し、プレフィックスを付けて区別しています - これらを足し合わせて複合モデル(
composite_model)を作成しています
- ガウシアンモデル(
- パラメータの初期設定:
make_paramsメソッドでパラメータオブジェクトを作成- ガウス関数の中心(
gauss_center)を5に設定し、0〜10の範囲に制限 - 標準偏差(
gauss_sigma)を2に設定し、正の値のみ許可 - 振幅(
gauss_amplitude)を3に設定し、正の値のみ許可 - 線形部分の傾き(
line_slope)を0.1に設定 - 切片(
line_intercept)を0に設定
- フィッティングの実行:
fitメソッドを使用して、xとyのデータに対してモデルをフィッティング- 結果は
resultオブジェクトに格納されます
- 結果の表示:
fit_reportメソッドで詳細なフィッティング結果を表示します- これには最適化されたパラメータ値、標準誤差、統計量などが含まれます
このコードは、前のセクションで生成したサンプルデータ(ガウス関数と線形関数の組み合わせ+ノイズ)に対して、同じ形式のモデルをフィットさせています。初期パラメータは、データ生成時に使用した真の値に近い値を設定しています。
信頼区間と予測区間の計算
lmfitの eval_uncertainty メソッドを使って、95%信頼区間を簡単に計算できます。また、予測区間は誤差の分散を考慮して計算します。
- より密なx値の生成:
x_dense = np.linspace(0, 10, 200)元のデータは100点でしたが、滑らかな曲線を描くために200点の密なグリッドを作成しています。 - フィットモデルの評価:
y_fit = result.eval(x=x_dense)先ほど得られたフィッティング結果を使って、密なx値に対するモデル予測値を計算しています。 - 信頼区間の計算:
dely = result.eval_uncertainty(x=x_dense, sigma=2)lmfitのeval_uncertaintyメソッドを使用して95%信頼区間(2シグマ)を計算しています。これはモデルの平均応答に関する不確実性を表します。 - 残差の標準偏差の計算:
sigma_res = np.sqrt(np.sum(result.residual**2) / (len(y) - len(result.params)))モデルの残差(実測値と予測値の差)から標準偏差を計算しています。分母は自由度(データ点数からパラメータ数を引いた値)を考慮しています。 - 予測区間の計算:
pred_interval = np.sqrt(dely**2 + sigma_res**2)予測区間は「信頼区間の不確実性」と「残差の分散」を組み合わせて計算します。これは新しいデータポイントの予測に関する不確実性を表し、通常は信頼区間より広くなります。
結果の可視化
Matplotlibを使って、モデルフィットの結果と不確実性を視覚化しました。詳細に解説します:
- 図の初期化:
fig,ax=plt.subplots()– 新しい図とサブプロットを作成します - 元データのプロット:
ax.scatter(x, y, color='black', label='データ')– 散布図として黒い点で元のデータポイントを表示します - フィットモデルのプロット:
ax.plot(x_dense, y_fit, 'r-', label='フィットモデル')– フィッティングされたモデルを赤い実線で表示します - 信頼区間の可視化:
ax.fill_between(x_dense, y_fit-dely, y_fit+dely, color='red', alpha=0.2, label='95% 信頼区間')– モデルの95%信頼区間を半透明の赤色で塗りつぶします - 予測区間の可視化:
ax.fill_between(x_dense, y_fit-pred_interval, y_fit+pred_interval, color='blue', alpha=0.1, label='95% 予測区間')– 予測の95%信頼区間を半透明の青色で塗りつぶします - グラフの装飾:
ax.legend(loc='best')– 凡例を最適な位置に配置ax.set_xlabel('X')とax.set_ylabel('Y')– 軸ラベルの設定ax.set_title('モデルフィットと不確実性区間')– グラフのタイトル設定ax.grid(True)– グリッド線の表示
- 図の表示:
plt.show()– 完成したグラフを表示します
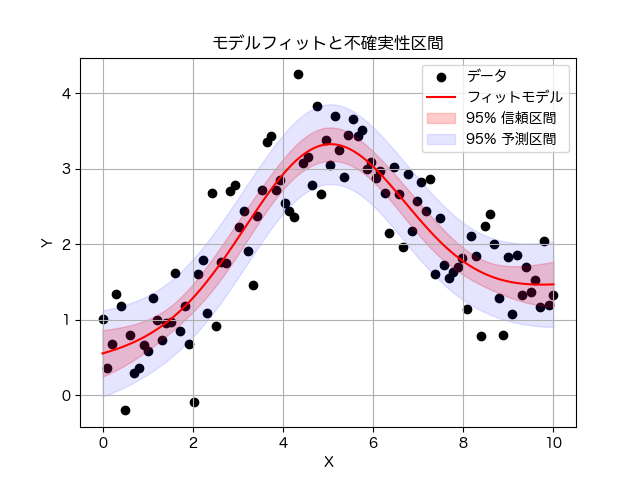
このグラフでは、黒い点が元データ、赤い線がフィットモデル、薄赤色の領域が95%信頼区間(モデルの不確実性)、薄青色の広い領域が95%予測区間(新しいデータの予測範囲)を示しています。予測区間は信頼区間より広くなっていることが視覚的に分かります。
まとめ
この記事では、lmfitを使用してモデルフィッティング後の不確実性を定量化し、視覚化する方法を紹介しました。特に:
- lmfitの
eval_uncertaintyメソッドを使うことで、95%信頼区間を簡単に計算できる - 予測区間は、信頼区間に残差の分散を加えることで計算できる
これらの手法を使うことで、モデルの予測がどの程度信頼できるかを定量的に評価でき、より堅牢なデータ分析が可能になります。
このようなアプローチは、科学研究や機械学習モデルの評価において、単なる点推定を超えた情報を提供し、モデルの信頼性を適切に評価するのに役立ちます。

コメント