[lmfit] 6. 2次元ガウス関数によるカーブフィッティング

はじめに

この記事では、lmfitライブラリを使用して2次元ガウス関数による非線形最小二乗フィッティングを行う方法について詳しく説明します。以下の内容を取り扱います：

• フィッティング結果の可視化と評価
• 2次元ガウス関数の数学的定義と理解
• lmfitによるモデルの構築方法
• パラメータの初期値設定と制約条件の適用

コード

解説

モジュールのインポートなど

バージョン

2dガウス関数の定義

x,yに相関のないガウス関数を定義します。

データの生成

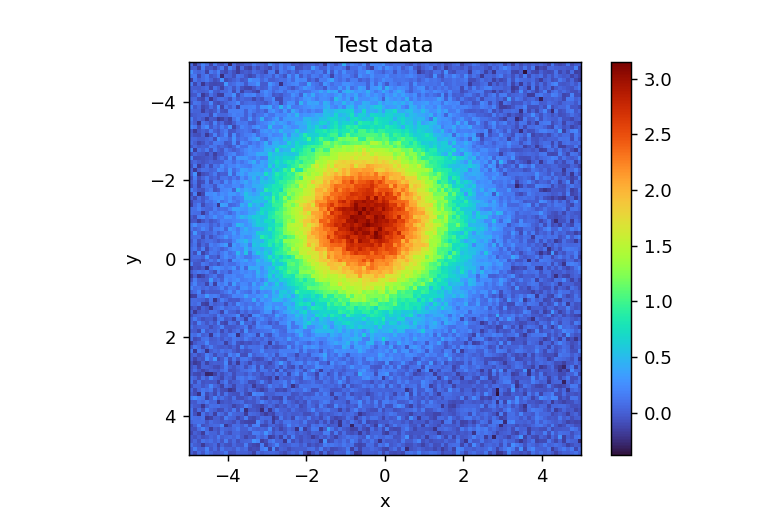
x, y 座標は np.meshgrid 関数で2次元格子を生成し、gaussian2D 関数を用いてデータを作成しました。また、np.random.normal(scale=.1,size=x.shape) を使用して現実的なノイズを加えています。

データを図示すると以下のようになります。

残差を返す関数の定義

初期値の設定

カーブフィット

最初にMinimizerオブジェクトを作成します。残差関数、初期パラメータ、そしてfcn_argsで残差関数に渡す引数を設定します。

次に、fit.leastsq()メソッドを使用してLevenberg-Marquardt法による最小化を実行し、近似を行います。

フィッティング完了後のパラメータ値は以下のようになります。

フィッティング結果の表示

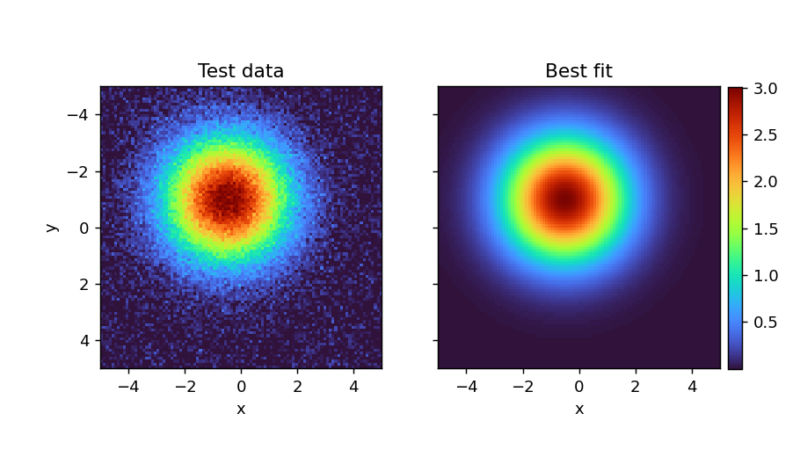
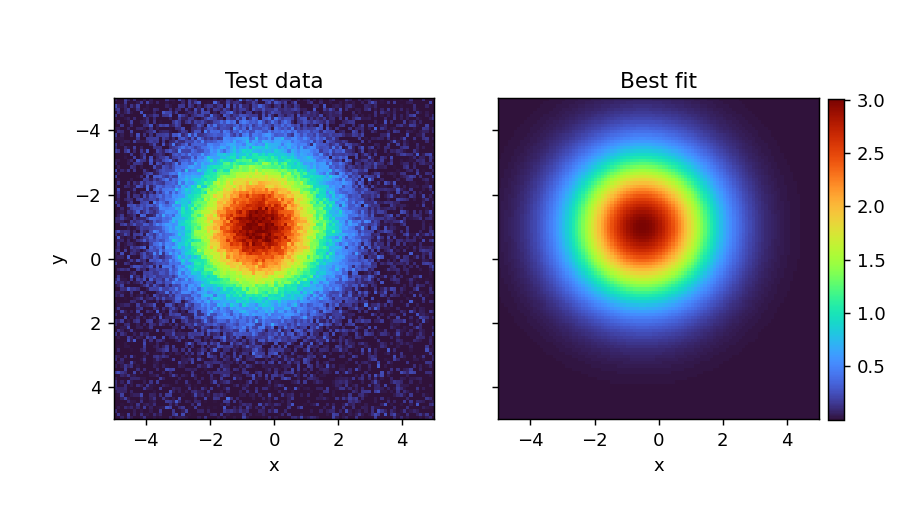
ベストフィットデータは data.flatten() – out.residual で取得できます。out.residual は1次元データなので、まず1次元でベストフィットデータを計算し、その後 reshape 関数を使って元の形状に戻します。

左側が元データ、右側がベストフィットデータです。カラーバーはinset_axes機能を使用して挿入しています。inset_axesの詳細については下記記事で解説しています。

[matplotlib] 79. inset_axesでカラーバーを自由自在に配置する

matplotlibのimshowで表示した画像に対して、inset_axes関数を使用してカラーバーを任意の位置に配置する方法を解説。位置やサイズを細かく調整し、美しいグラフ表現を実現するテクニックを紹介します。

sabopy.com

2020.05.08

ベストフィットデータを得る別の方法

パラメータはout.params['height']のような形式で参照できるため、これらのベストフィットパラメータを関数に適用することでもベストフィットデータを生成できます。

コードをダウンロード(.pyファイル) コードをダウンロード(.ipynbファイル)

参考

Non-Linear Least-Squares Minimization and Curve-Fitting for Python — Non-Linear Least-Squares Minimization and Curve-Fitting for Python

lmfit.github.io

2D Gaussian fit using lmfit

I need to fit a two dimensional Gaussian to a data set I read in. My choice of fitting routine is lmfit, as it allows ea...

stackoverflow.com