はじめに
この記事では、空気抵抗とマグヌス効果を考慮した斜方投射問題を解くために、SciPyのsolve_ivp関数を使用する方法を解説します。以下の内容を取り上げます:
- 空気抵抗とマグヌス効果を含む物理モデルの数学的定式化
- 常微分方程式を解くためのsolve_ivp関数の使い方
- 複雑な物理系のPythonによる実装方法
- 結果の可視化と物理的解釈
物理学の知識とPythonプログラミングを組み合わせた実践的な例を通して、数値計算の基本を学びましょう。
マグヌス効果とは
マグヌス効果(Magnus effect)とは、回転している物体が流体中を移動する際に、回転方向と相対的な流れの方向によって物体に働く力のことです。物理学者ハインリヒ・マグヌスにちなんで名付けられました。
簡単に言えば、回転するボールが飛行中に「曲がる」現象の物理的な説明です。この効果は以下のように説明されます:
- 回転するボールの周りの空気の流れが、回転方向によって非対称になる
- 回転方向と同じ向きの側では空気の流れが速くなり、反対側では遅くなる
- ベルヌーイの原理により、流れが速い側は圧力が低く、遅い側は圧力が高くなる
- この圧力差により、ボールには回転軸に垂直な方向に力(マグヌス力)が働く
スポーツでは以下のような現象として観察されます:
- 野球のカーブボール:投手が与える回転によって軌道が曲がる
- サッカーのカーブシュート:キッカーが与える回転によってボールが曲がる
- ゴルフのスライスやフック:クラブがボールに与える回転により飛球が曲がる
- 卓球のスピン:ラケットの角度と動きによってボールに様々な回転が与えられる
コード
解説
モジュールのインポート
バージョン
初期値の設定
初期値v0を設定します。位置(x,y)=(0,10)から速度(vx,vy)=(10,10)で物体を打ち上げる条件としました。
定数を定義
ここで、mは質量、kは抗力係数、gは重力加速度です。sはマグヌス効果の係数であり、wは回転ベクトルで(0,0,1)と設定しました。
関数の定義
微分方程式を定義します。運動の第2法則から以下の式が導かれます。
\[m \cdot u” = F + mg\]
空気抵抗による力は F = -ku’ で表されます。また、マグヌス効果による力は、角速度ベクトル ω=(0,0,1) とすると、s(−ωvy, ωvx, 0) となります。これらを運動方程式に変換すると、以下のようになります。
\[u_x” = -\frac{k}{m} u_x’ -\frac{s}{m} u_y’ \]
\[u_y” = -\frac{k}{m} u_y’ +\frac{s}{m} u_x’+ g\]
solve_ivpで解く
t_spanは時間の(開始、終了)を表し、tは実際の計算に使用する時間配列です。t_evalにtを指定しますが、省略した場合はsolve_ivpが自動的に適切な時間間隔で計算を行います。その他のパラメータはargs=(k,s,w)のように引数として渡します。v0は初期条件を表します。
solve_ivp(f, t_span, v0, t_eval=t, args=(k,s,w))を呼び出して微分方程式を解きます。
計算が正常に完了したかどうかは、返り値のmessage属性で確認できます。
結果の表示
ここでは「ind = solved_data.y[1]>=0」という条件でyが正の値のみを抽出して表示しています。解析結果のデータは「solved_data.y[0][ind]」のような形式で取得できます。
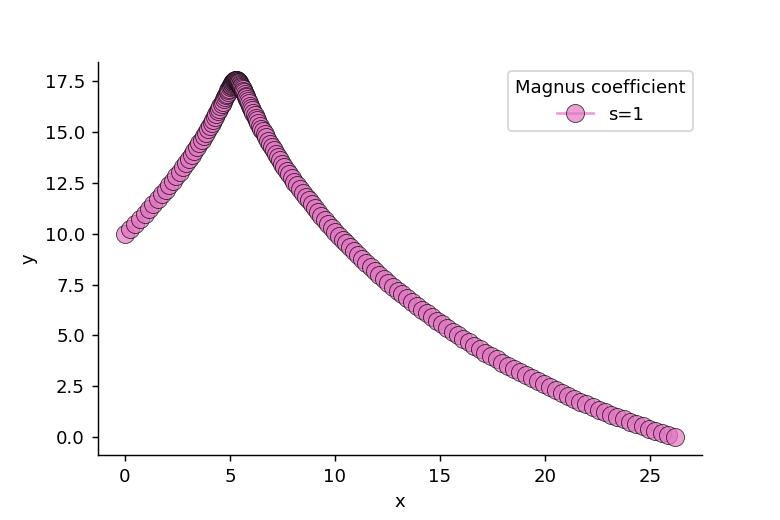
マグヌス係数s=1の場合のxとyの関係は以下のようになります。
sを変えた時の変化
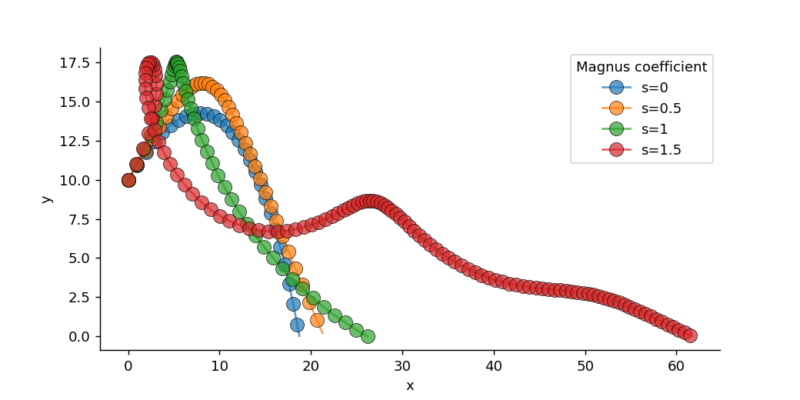
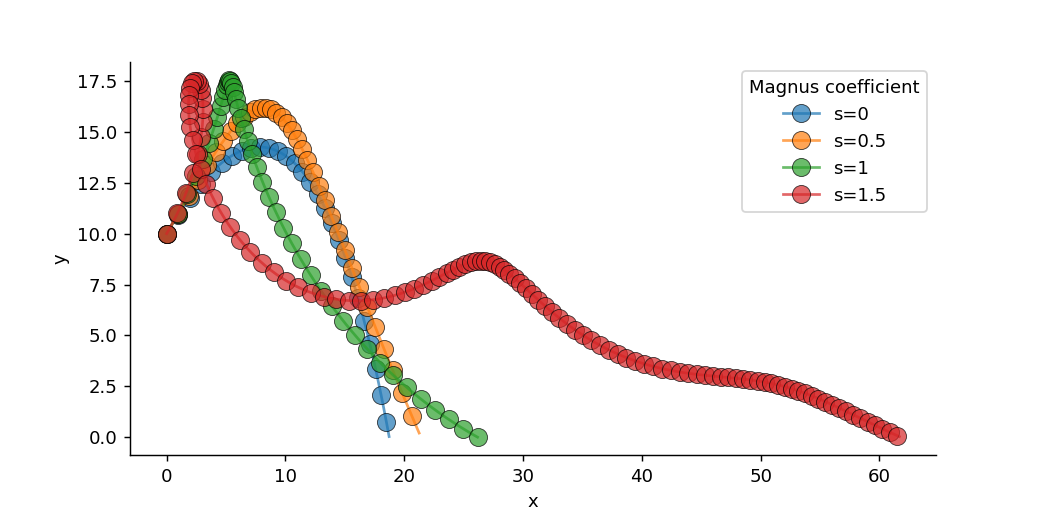
マグヌス係数sの値を[0, 0.5, 1, 1.5]と変化させて計算した結果は以下のようになります。

アニメーションによる結果の可視化
matplotlibのFuncAnimationを使用して、結果をアニメーションで可視化した例については、下記記事で詳しく解説しています。

参考


コメント