はじめに
この記事では、lmfitライブラリを使用してローレンツ分布関数モデルによる非線形カーブフィッティングを行う方法を詳しく解説しています。パラメータの設定方法、実際のコード実装例、そして結果の可視化まで、ステップバイステップで説明します。
コード
解説
モジュールのインポート
バージョン
データの生成
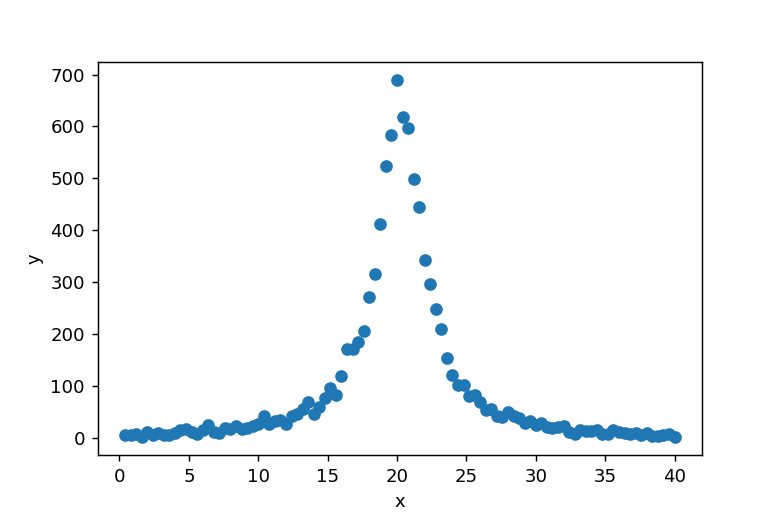
まず、stats.cauchy.rvs関数を使用してローレンツ分布に従うランダムなデータを生成します。このデータをヒストグラム化することでフィッティング対象のデータセットを作成します。以下の図はxとyの関係を示しています。
モデルの定義
lmfit.modelsモジュールのLorentzianModelをモデル関数として使用します。ローレンツ関数は次の式で表されます。ここでAは振幅、μは中心値、σは半値幅を表します。
\[f(x; A, \mu, \sigma) = \frac{A}{\pi} \big[\frac{\sigma}{(x – \mu)^2 + \sigma^2}\big]\]
初期パタメータの推定
model.guess(y, x=x)を使用して、上図のデータをローレンツ関数モデルで近似するためのフィッティングパラメータの初期値を推定します。推定されたパラメータ(params)は以下のようになります。
カーブフィット
model.fit(y, params, x=x)を実行してカーブフィッティングを行います。
フィッティング結果の表示
print(result.fit_report())でフィッティング結果の詳細を確認できます。
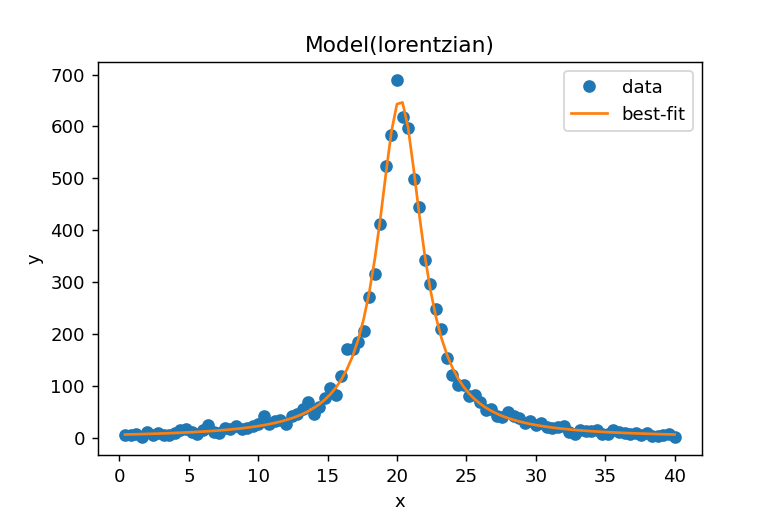
result.plot_fit()を使用すると、元のデータとフィッティングカーブが同一グラフ上に表示されます。

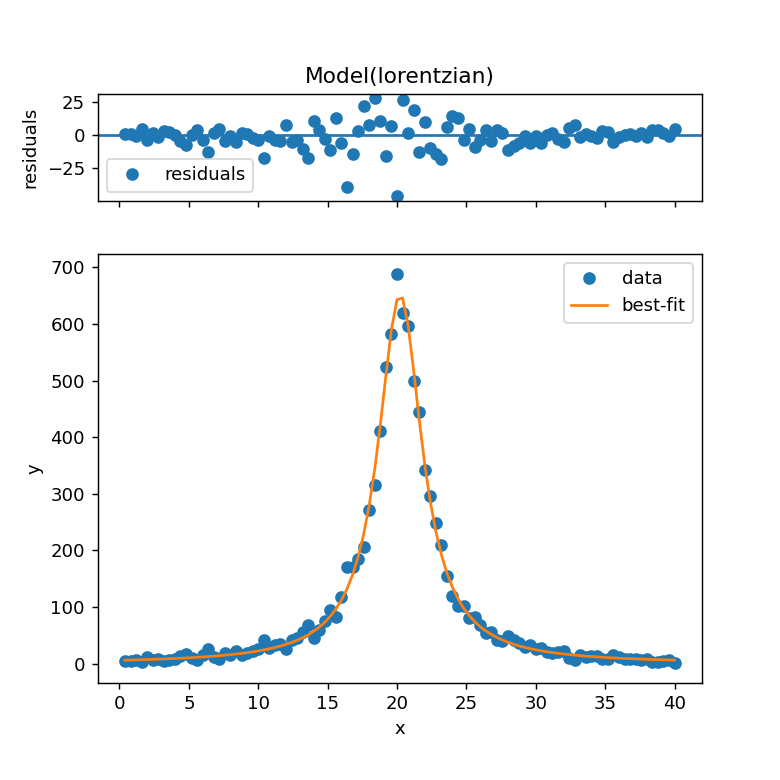
result.plot()とすることで残差とともにフィッティング結果が表示されます。
参考
Built-in Fitting Models in the models module — Non-Linear Least-Squares Minimization and Curve-Fitting for Python
scipy.stats.cauchy — SciPy v1.17.0 Manual

コメント