はじめに
2次元における反応拡散系の偏微分方程式(フィッツフュー-南雲モデル)を有限差分法で解く方法について説明する。
コード
解説
モジュールのインポート
バージョン
パラメータの設定
以下の偏微分方程式を用いる。
\[\begin{align*}
\frac{\partial u}{\partial t} &= a \Delta u + u – u^3 – v + k\
\end{align*}\]
\[\begin{align*}
\tau\frac{\partial v}{\partial t} &= b \Delta v + u – v
\end{align*}\]
係数のa,b,τ,kの値を設定する。
データサイズ、時間などの設定
nは計算回数で12/0.001なので12000回となる。時間ステップdtは小さくしないと解の安定性が悪くなる。
初期値の設定
np.random.rand(size, size)で形状が(100,100)の0〜1のランダムな値をもつ2D配列を作成する。
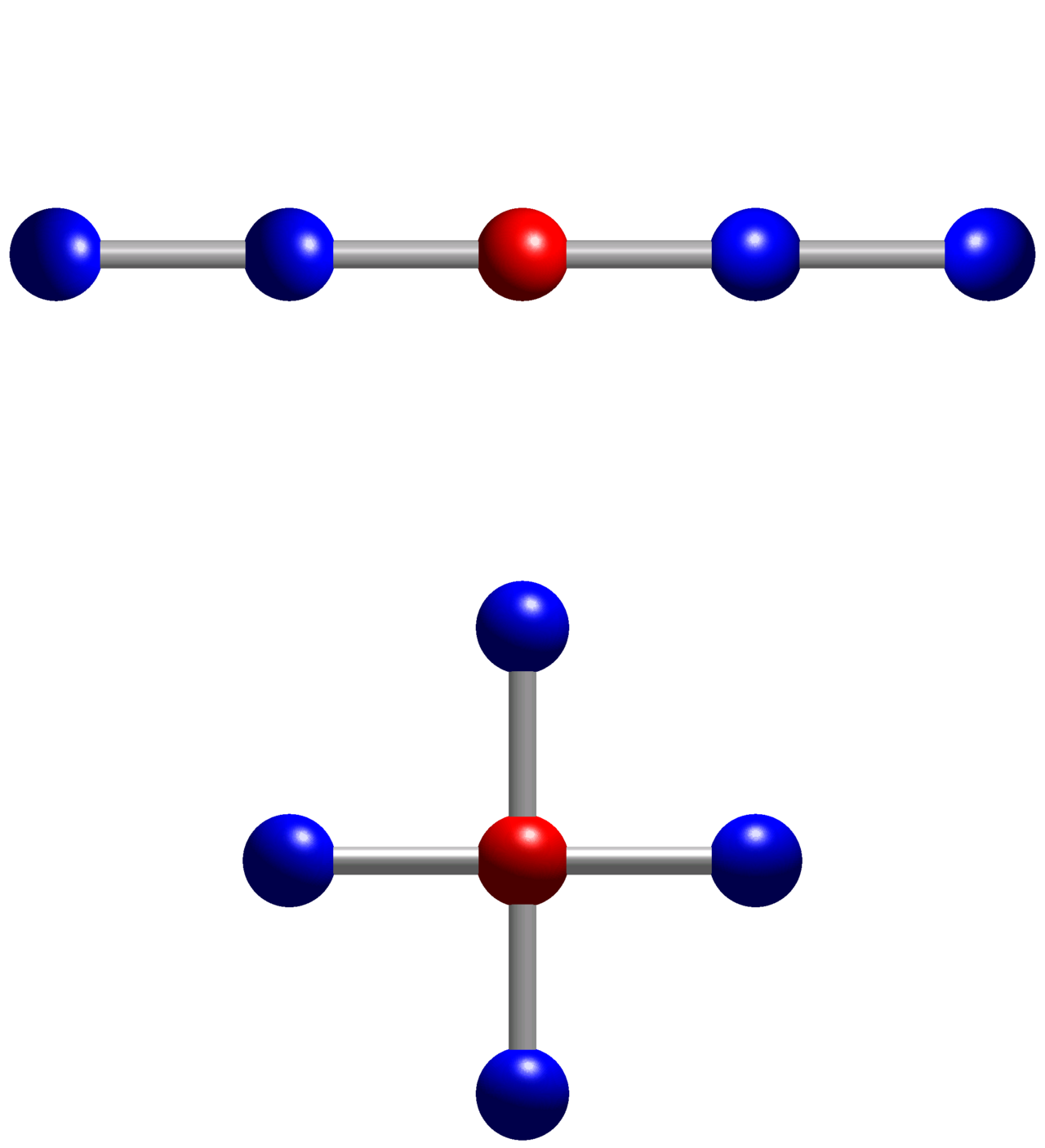
ラプラシアンを定義
5点ステンシルによって、2つの変数の関数のラプラシアンを近似する。
画像を表示する関数
figの準備
plt.subplots(4, 3)として12個の画像を示す。
偏微分方程式を有限差分法で解く
最初に、laplacian(U)でラプラシアンを計算する。
次に、Uc = U[1:-1, 1:-1]でエッジを除く部分をUcとする。
U[1:-1, 1:-1] = Uc + dt * (a * deltaU + Uc – Uc**3 – Vc + k)と
V[1:-1, 1:-1] = Vc + dt * (b * deltaV + Uc – Vc) / tauにより、UとVの値を更新する。
ノイマン境界条件の適用を適用するために、エッジの部分をその一つ内側の要素と同じ値とする。
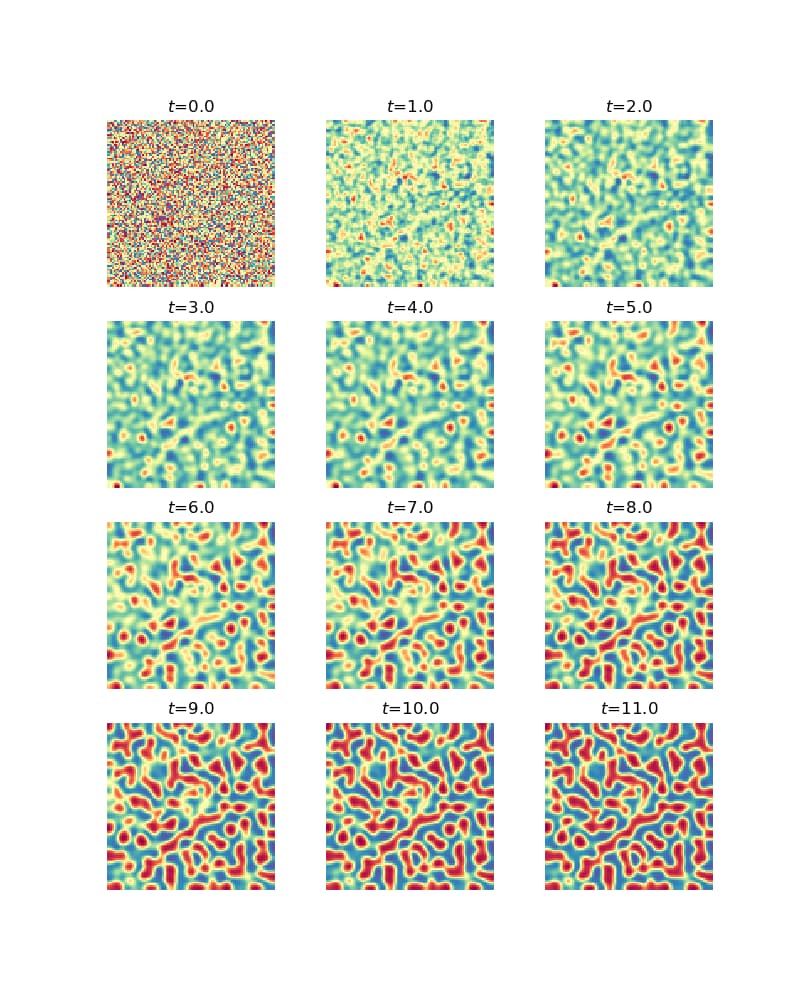
結果の表示
if i % step_plot == 0 and i < 12*step_plot:でi÷step_plot(1000)のあまりが0の時に画像を表示するようにする。タイトル部分にその時のtの値を表示する。
参考
コメント