はじめに
偏微分方程式（PDE）は、自然現象や工学的問題を記述する上で重要な役割を果たしています。本記事では、特に反応拡散系の一種であるフィッツフュー-南雲モデルを例に取り、有限差分法を用いた数値解法について解説します。SciPyを活用したPDEの解き方、境界条件の設定方法、数値安定性の確保など、実装に必要な知識を順を追って説明していきます。
コード
解説
モジュールのインポート
バージョン
パラメータの設定
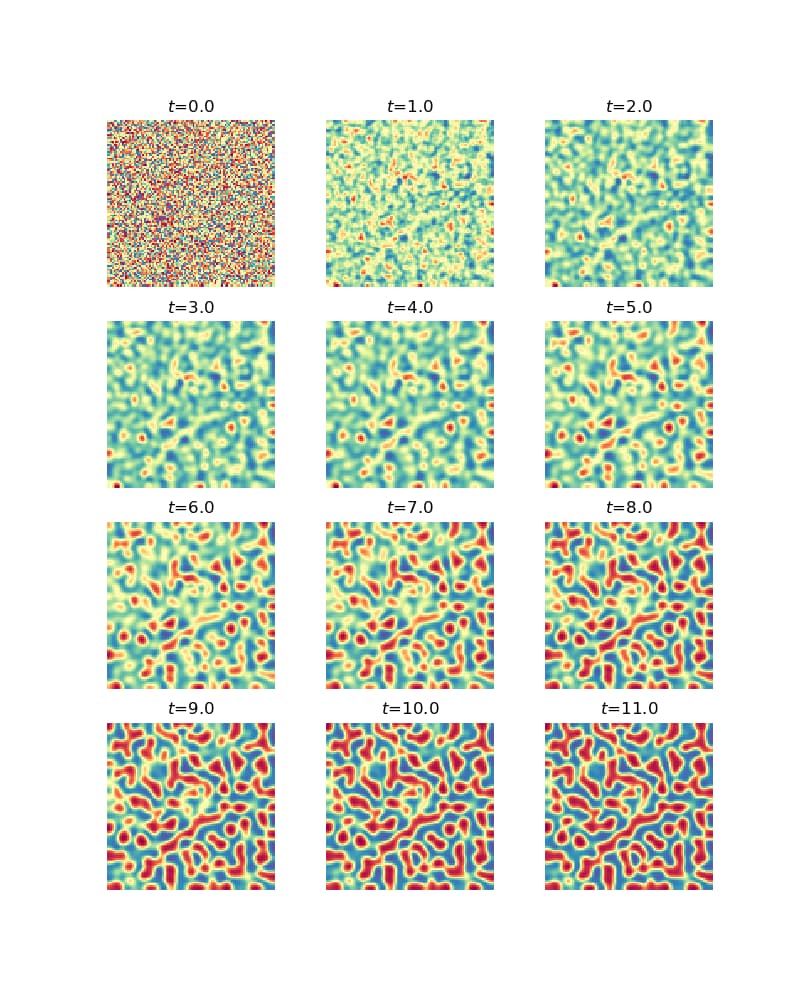
以下の偏微分方程式を用います。
\[\begin{align*}
\frac{\partial u}{\partial t} &= a \Delta u + u – u^3 – v + k\
\end{align*}\]
\[\begin{align*}
\tau\frac{\partial v}{\partial t} &= b \Delta v + u – v
\end{align*}\]
係数のa,b,τ,kの値を設定します。
データサイズ、時間などの設定
nは計算回数であり、12/0.001から12000回と算出されます。時間ステップdtは十分に小さくしなければ、解の安定性が損なわれます。
初期値の設定
np.random.rand(size, size)を使用して、形状が(100,100)の0〜1の範囲にあるランダムな値を持つ2次元配列を生成します。
ラプラシアンを定義
5点ステンシルを用いて、2変数関数のラプラシアンを近似します。5点ステンシルとは、有限差分法において、2変数関数のラプラシアン（二階偏微分）を数値的に近似するための手法です。関数の値とその周囲4点（上下左右）の値を使用して、差分方程式を構築します。この方法は偏微分方程式を数値的に解く際の基本的なテクニックの一つです。
画像を表示する関数
figの準備
plt.subplots(4, 3)を使用して12個のグラフを表示します。
偏微分方程式を有限差分法で解く
まず、laplacian(U)を使用してラプラシアンを計算します。次に、Uc = U[1:-1, 1:-1]により格子の内部領域（エッジを除いた部分）をUcとして取り出します。
そして、U[1:-1, 1:-1] = Uc + dt * (a * deltaU + Uc – Uc**3 – Vc + k)という式で、V[1:-1, 1:-1] = Vc + dt * (b * deltaV + Uc – Vc) / tauという式で、UとVの値を更新します。ノイマン境界条件を適用するために、エッジ部分をその一つ内側の要素と同じ値に設定します。
結果の表示
if i % step_plot == 0 and i < 12*step_plot:という条件で、iをstep_plot(1000)で割ったあまりが0の時に画像を表示します。また、各グラフのタイトル部分にはその時点のt値を表示する。
まとめ
本記事では、フィッツフュー-南雲モデルという反応拡散系の偏微分方程式を有限差分法で解く方法を解説しました。SciPyライブラリを活用した実装方法、境界条件の設定、時間発展の計算手法について詳細に説明しました。この手法は様々な物理現象のシミュレーションに応用可能であり、計算科学における基礎的なスキルとなります。今回学んだ手法を発展させることで、より複雑な系への応用も可能になるでしょう。
参考
コメント