はじめに
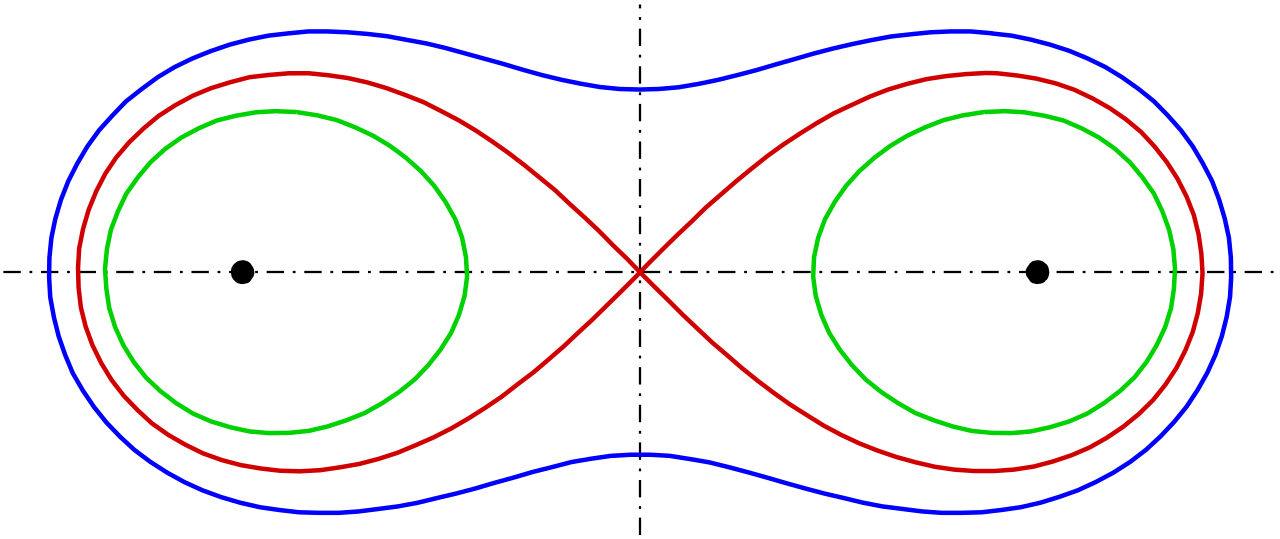
本記事はmatplotlibのFuncAnimationを使って、カッシーニの卵形線(Cassini oval)のアニメーションを作成する方法を解説します。カッシーニの卵形線は、2つの固定点からの距離の積が一定となる点の軌跡です。記事ではPythonのコードとともに、アニメーションの実装手順を詳細に説明します。
コード
解説
モジュールのインポート
グリッドと軸ラベル、アスペクト比の設定
卵形線データの生成
卵形線は下記の式のように定義されます。
$$(x^2+y^2)^2 -2a^2(x^2–y^2) = k^4 – a^4$$今回は、媒介変数(極座標)で卵形線のデータを生成します。 θ(t)を0〜2πの範囲、パラメータaをa=1に固定し、 パラメータkを順次変化させたアニメーションを作成します。 なお、cとsはそれぞれcos(t)とsin(t)を表しています。
卵形線を媒介変数表示すると以下のようになります。
$$r^2 = a^2cos2\theta \pm \sqrt{a^4cos^2 2\theta +k^4 – a^4}$$rには±の記号があるため、平方根(√)が正の場合をr_p_pとし、平方根が負の場合をr_p_mとしています。
それぞれのrの値を用いて、x座標とy座標のデータを計算しています。
アニメーションを表示するための設定
アニメーション用に表示するグラフを格納する空のリスト「tamagos」と「tamagoss」を作成します。
アニメーションの設定
アニメーションでは古いプロットを消す必要があるため、グラフのリスト(tamagos、tamagoss)にグラフが入っている場合は、pop().remove()メソッドで削除します。
r_p_pとr_p_mを使用して、異なるk値のデータを順次作成し、それぞれのrからx、y座標を生成してプロットします。「go」で緑色の丸、「mo」でマゼンタ色の丸として表示されます。
作成したプロットを空のリスト(tamagos、tamagoss)に格納することでアニメーション表示が可能になります。
ax.set_title(“cassini, parameter $a$= “+str(a)+”, $k$= “+str(k[num])[:4]+””)を使用して、タイトルにアニメーションで変化するkの値をリアルタイムに表示します。[:4]の指定により、小数点以下の桁数が多すぎるのを防いでいます。
アニメーションの表示
FuncAnimationを使用してアニメーションを表示します。updateを200ステップ実行してアニメーションを生成します。intervalは100msに設定されているため、合計で20秒のアニメーションになります。
HTML(ani.to_html5_video())関数を使うことで、Jupyter Notebook上に直接アニメーションを表示できます。
アニメーションの保存
ani.save(‘filename.mp4’, writer=”ffmpeg”, dpi=dpi)でアニメーションを保存できます。dpiを設定することで、希望する解像度での保存が可能になります。
コードをダウンロード(.pyファイル) コードをダウンロード(.ipynbファイル)まとめ
matplotlib.animation.FuncAnimationを活用することで、数学的な曲線であるカッシーニの卵形線のダイナミックなアニメーション表現が可能になります。このテクニックは、様々な数学的図形や物理現象の視覚化に応用できるでしょう。
参考

コメント