[SciPy] 1. Scipyのcurve_fitで最小2乗法近似、決定係数R2も求める

はじめに
コード
解説
誤差を大きくした時の近似結果の変化
参考

はじめに

pythonのscipyのcurve_fitによる、曲線当てはめのやり方、決定係数R²の求め方について説明する。

コード

解説

モジュールのインポート

バージョン

データの生成

np.linespaceは(-1,1,20)の場合、-1から1まで20個の連続した配列を生成する。
np.random.rand(1)は 0〜1の範囲で乱数を1個生成する。ここでは1次関数の係数ををランダム値で取得した。
np.random.normal()は標準正規分布の乱数でsizeをlen(x_data)としてx_dataと同じ20個の配列を生成した。[1]

近似式を定義

近似に用いる関数を定義する。[2]

curve_fitで近似

x_dataとy_data_1を関数funcでフィッティングする。poptが最適推定値で、np.random.rand()で得た値の近似値となる。pcovは共分散となる。[3]

R2の計算

決定係数(r_squared)は１に近いほど、その近似がもっともらしい。
residualsはデータと近似曲線の差(残差)をとっている。
rssはresidual sum of squaresの略で残差の２乗の合計、tssはtotal sum of squaresの略で各y_dataとy_dataの平均の差の２乗の合計で、データそのもののばらつきを表す。[4]

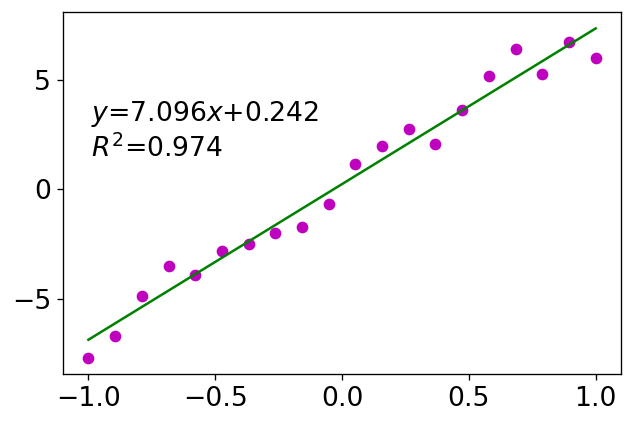
dataを点, 近似結果を線でプロット

‘mo’はマゼンダ(m)のo(丸)でプロットするという意味となり、’g-‘はグリーン(g)の線でプロットするという意味となる。

この方法で指定できる色は{'b', 'g', 'r', 'c', 'm', 'y', 'k', 'w'}に限られている。[5]

誤差を大きくした時の近似結果の変化

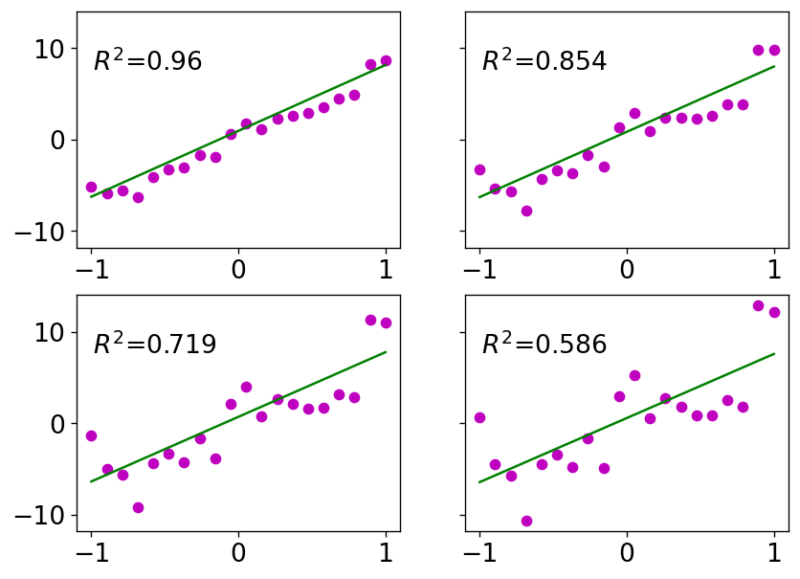
エラーを2, 3, 4倍にしたときのフィッティングの変化の様子をみた。

結果は以下のようになる。左上がエラー1倍、右上がエラー2倍、左下がエラー3倍, 右下がエラー4倍のときの結果となる。

誤差の増加によって、R²が低下したことから、R²は正しく計算されていると言える。

コードをダウンロード(.pyファイル)

コードをダウンロード(.ipynbファイル)

参考

https://amzn.to/3oRZunR

[SciPy] 1. Scipyのcurve_fitで最小2乗法近似、決定係数R²も求める