はじめに
フォークト分布関数とは、ガウス分布関数とローレンツ分布関数の畳み込み積分によって表される分布関数です。特に分光学の分野では、スペクトルピークの形状をモデル化する際によく使用されます。本記事では、Pythonのlmfitライブラリを用いてフォークト分布関数によるカーブフィッティングを実装する方法を解説します。
コード
解説
モジュールのインポート
バージョン
データの生成
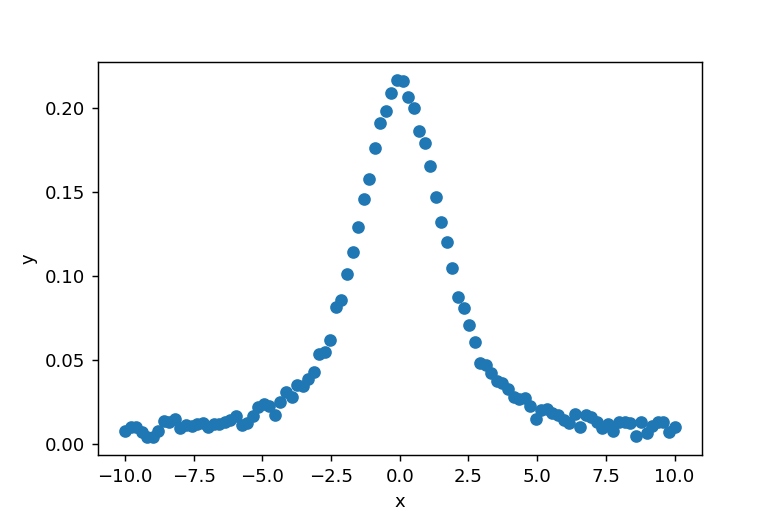
SciPyのspecial.voigt_profileを使用してフォークト分布のラインプロファイルを作成します。rng = default_rng()を設定し、rng.random(100)でノイズを追加します。xとyの関係を図示すると以下のようになります。
モデルの定義
lmfit.models モジュールのVoigtModel をモデル関数として使用します。Voigt関数は特定の式で表され、パラメータとして amplitude(振幅)、center(中心)、sigma(シグマ)、およびgamma(ガンマ)を持ちます。
\[f(x; A, \mu, \sigma, \gamma) = \frac{A \textrm{Re}[w(z)]}{\sigma\sqrt{2 \pi}}\]
\[\begin{eqnarray*}
z &=& \frac{x-\mu +i\gamma}{\sigma\sqrt{2}} \\
w(z) &=& e^{-z^2}{\operatorname{erfc}}(-iz)
\end{eqnarray*}\]
初期パタメータの推定
model.guess(y, x=x)を使用して、上図のデータをフォークト関数モデルで近似するためのフィッティングパラメータの初期値を推定します。これにより得られるパラメータ(params)は以下のようになります。
カーブフィット
model.fit(y, params, x=x)により、カーブフィッティングを実行します。
フィッティング結果の表示
print(result.fit_report())を実行することで、フィッティングの詳細な結果を確認できます。
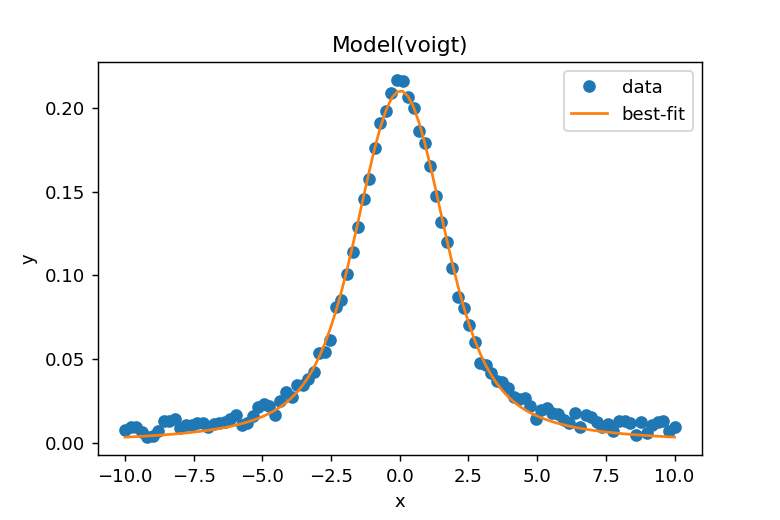
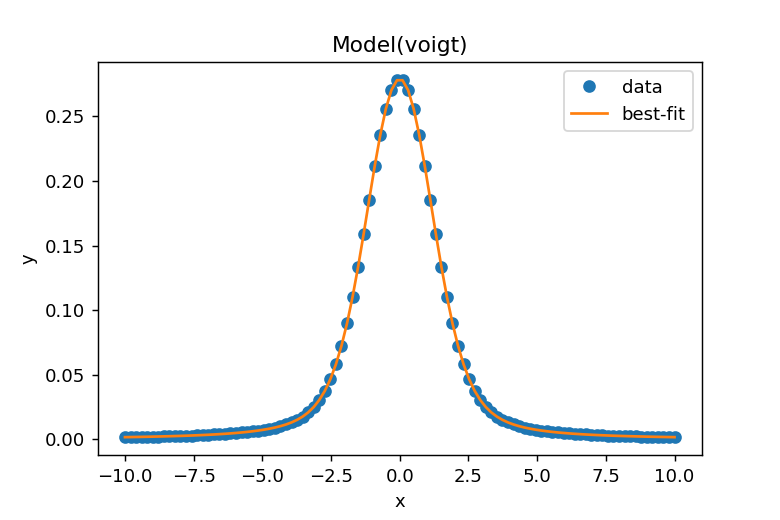
result.plot_fit()によりデータとフィッティングカーブが表示されます。

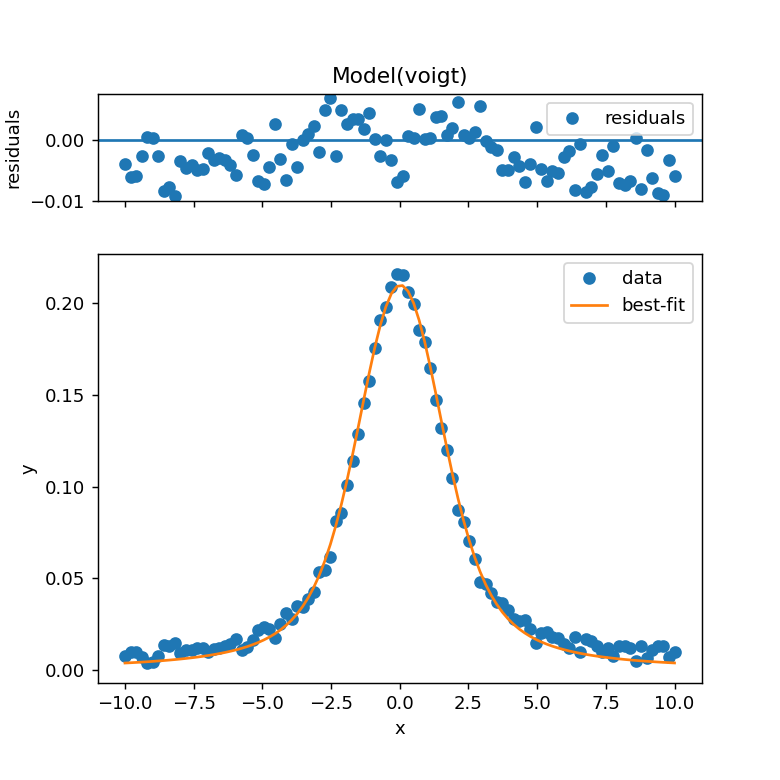
result.plot()を実行すると、フィッティング結果とその残差が同時にグラフ表示されます。
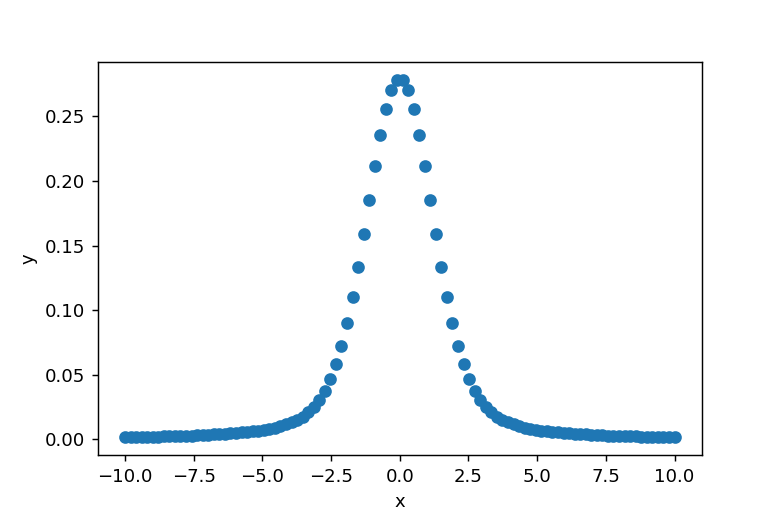
sigmaとgammaの値が異なる場合
デフォルトではsigmaとgammaの値は同じに設定されています。gammaの値を自由に変更してフィッティングしたい場合は、params[‘gamma’].set(vary=True) と指定する必要があります。
まとめ
lmfitライブラリを使用したフォークト分布関数モデルによるカーブフィッティングは、スペクトル解析やピーク形状の分析に非常に有効です。パラメータの制約や複数ピークの同時フィッティングなど、lmfitの柔軟な機能を活用することで、より精密なデータ分析が可能になります。
また、フィッティング結果から得られた統計情報(AIC、BIC、カイ二乗値など)を比較することで、複数のモデル間での適合度を客観的に評価することもできます。科学的なデータ解析において、このような定量的な評価は非常に重要です。

コメント