はじめに
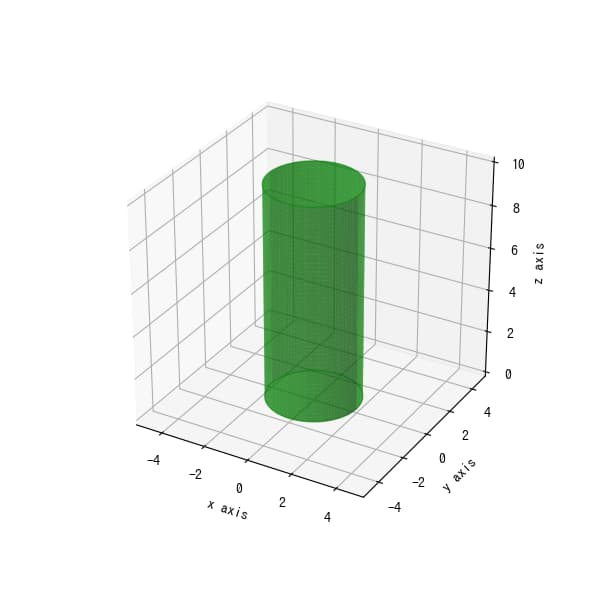
本記事はMatplotlibを使用した3D空間での円柱の描画方法を解説しています。直交座標系における円柱の数学的定義から始まり、具体的なPythonコードによる実装方法を説明します。
コード
解説
モジュールのインポート
from mpl_toolkits.mplot3d import Axes3D
import mpl_toolkits.mplot3d.art3d as art3d
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Circle
3Dグラフにする設定
fig=plt.figure(figsize=(6,6)) ax = fig.gca(projection='3d')
データ生成
x = np.linspace(-2, 2,100)
z = np.linspace(0, 10, 100)
X, Z = np.meshgrid(x, z)
Y = np.sqrt(2**2 - X**2)
半径2、高さ10の円柱を作成します。X軸とZ軸でmeshgridを作成し[1]、Y軸の値はピタゴラスの定理を用いて算出します[2]。
プロットの作成
ax.plot_surface(X, Y, Z, linewidth=1, color='g',alpha=0.5)
ax.plot_surface(X, -Y, Z, linewidth=1,color='g',alpha=0.5)
円柱の描画では+Y方向と-Y方向の両面をプロットする必要があります。例えば、color=’g’パラメータで緑色に、alpha=0.5で透明度50%のsurfaceグラフを作成できます。
蓋の作成
#Draw lid
futa = Circle((0, 0), 2,fc='g',ec='g',alpha=0.5)
ax.add_patch(futa)
art3d.pathpatch_2d_to_3d(futa, z=10, zdir="z")
Circleパッチを使用して、半径2、中心座標(0,0)の円を作成します。
ax.add_patchメソッドでこの円をグラフに追加します。
pathpatch_2d_to_3d関数を使用することで、2次元の円パッチを3Dグラフ上に表示できます。
この円は円柱の蓋として機能するため、表示位置はz=10、方向はzdir=”z”と指定します。
底の作成
#Draw bottom
soko = Circle((0, 0), 2,fc='g',ec='g',alpha=0.5)
ax.add_patch(soko)
art3d.pathpatch_2d_to_3d(soko, z=0, zdir="z")
同様に底も作成します。底の位置は、z=0、zdir=”z”と指定します。
軸ラベル、軸範囲の設定
ax.set_xlabel('x axis')
ax.set_ylabel('y axis')
ax.set_zlabel('z axis')
ax.set_xlim(-5,5)
ax.set_ylim(-5,5)
ax.set_zlim(0,10)
#ax.set_aspect('equal')
コードをダウンロード(.pyファイル)
コードをダウンロード(.ipynbファイル)

コメント