はじめに
この記事では、matplotlib の mplot3d を使用して3Dグラフ上に直方体(Cuboid)を表示する方法について解説します。3Dグラフィックスで立体的な直方体を描画する手法です。
コード
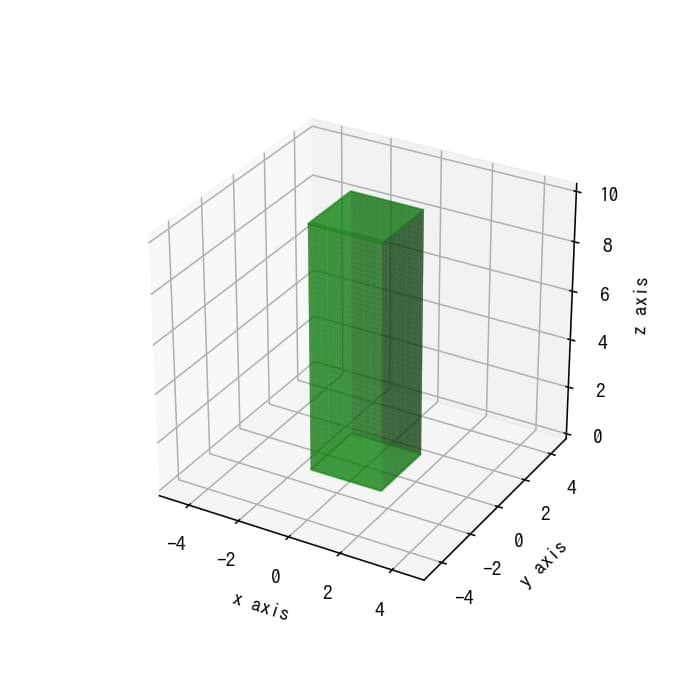
解説
モジュールのインポート
バージョン
3Dグラフの設定
データの生成
パラメータtはxy平面上の媒介変数を表し、zは高さ方向のデータを表します。tとzからmeshgridを作成することで、3次元空間でのプロットが可能になります。直方体の形状はスーパー楕円の式を用いて生成します。

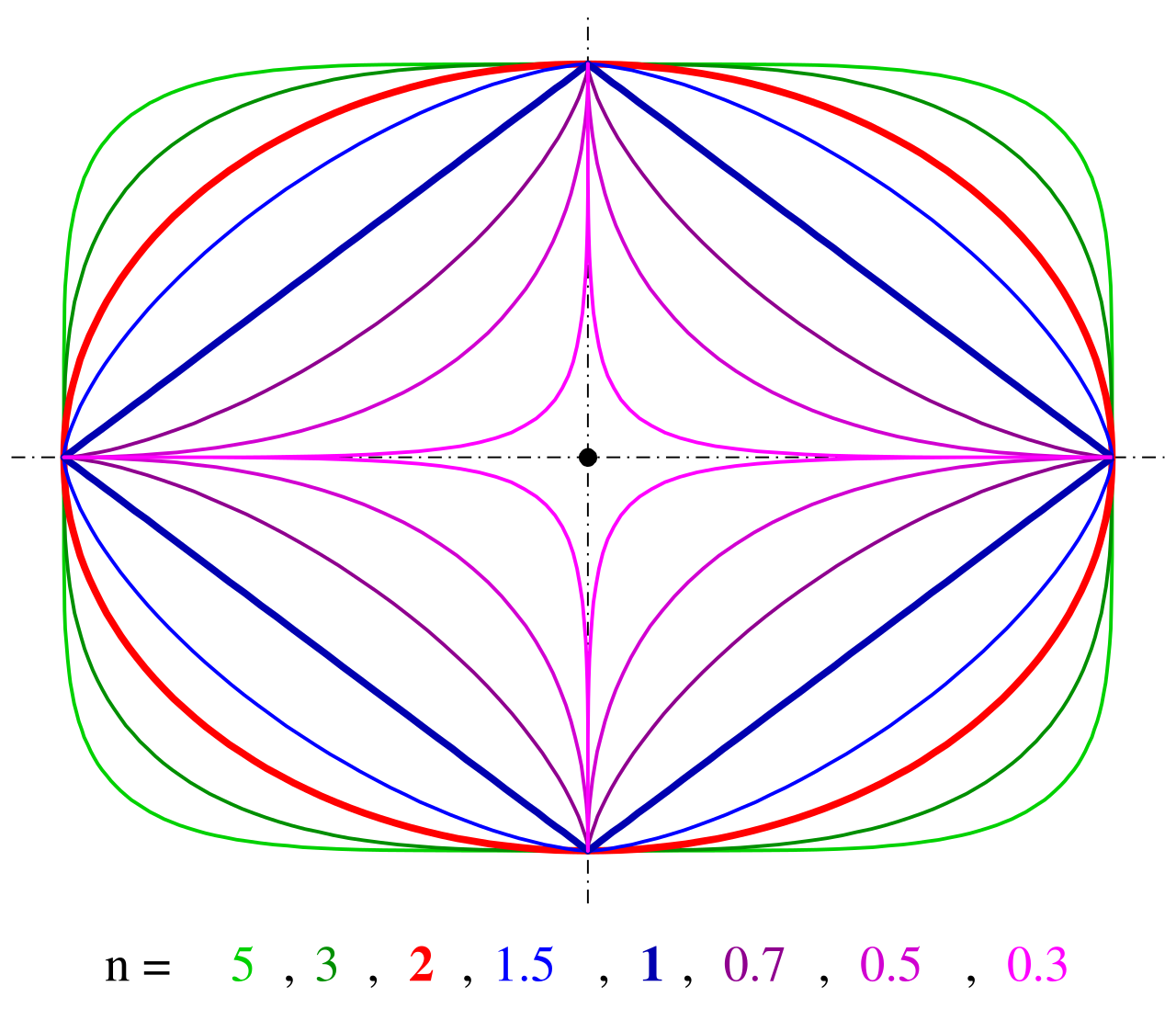
スーパー楕円は下記の式のように定義されます。
$$|\frac{x}{a}|^p + |\frac{y}{b}|^p = 1$$p=1のとき四角形になります。プロットするデータは媒介変数で生成します。媒介変数θ(t)は0〜2πの範囲を取ります。aはy=0におけるx軸の半径、bはx=0におけるy軸の半径です。ここでは、cとsはそれぞれcos(t)とsin(t)を表します。スーパー楕円を媒介変数表示すると以下のようになります。
$$x(t) = |cost|^\frac{2}{p}\cdot a sgn(cost)\\y(t) = |sint|^\frac{2}{p}\cdot b sgn(sint)$$直方体データの回転

前述と同じ回転方法を適用し、スーパー楕円で生成した四角形の各辺をx軸とy軸に平行にします。原点を中心に角度γだけ回転させた場合、x座標とy座標は以下のように表されます。
$$x’=xcos\gamma – ysin\gamma\\y’=xsin\gamma + ycos\gamma$$回転させた場合の図は以下のようになります。

底面と上面の設定
底面と上面はRectangleを使用して作成します。
Rectangleを使うと四角形を描画できます。xyパラメータで四角形の左下座標を指定し、widthで幅(x軸方向の長さ)、heightで高さ(y軸方向の長さ)を設定します。このコードではnp.min()とnp.max()を使ってこれらの値を設定しています。
2次元データを3次元空間上に表示するために、art3d.pathpatch_2d_to_3dを使用しました。zdir=”z”と設定し、zパラメータに表示したい高さを指定することで、任意の高さに四角形を配置できます。
軸範囲、軸ラベルの設定
3Dグラフの表示
回転アニメーション
作製した図を回転させると以下のようになる。
回転アニメーションは以下の記事を参考にして作成しました。

参考

コメント