はじめに
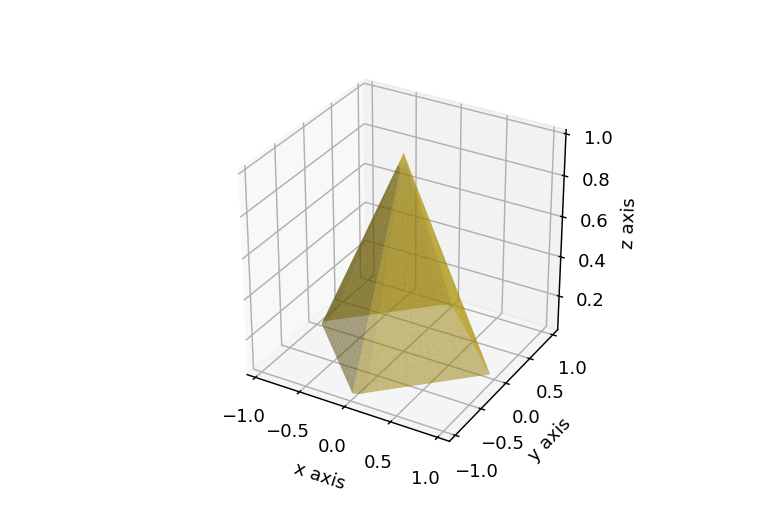
このページでは、Pythonのmatplotlibライブラリを使用して3D空間に四角錐（ピラミッド）を描画する方法について解説します。
コード
解説
モジュールのインポート
バージョン
3Dグラフの設定
データの生成
まずは2次元平面における4角形を考えましょう。2次元での正n角形は、tを媒介変数として0〜2πの範囲で表し、$$ a_n=\frac{2\pi}{n} $$とすると、
$$ x =\cos t \cdot \frac{\cos \frac{a_n}{2}}{\cos\left[a_n\left\{\frac{t}{a_n}-{\rm floor}\left(\frac{t}{a_n}\right)\right\}-\frac{a_n}{2}\right]}\\ y =\sin t \cdot \frac{\cos \frac{a_n}{2}}{\cos\left[a_n\left\{\frac{t}{a_n}-{\rm floor}\left(\frac{t}{a_n}\right)\right\}-\frac{a_n}{2}\right]} $$で表される。この式は下記サイトを参考にしました。
正多角形とスピログラフの数式
正多角形とスピログラフの数式です。 正多角形(2次元) 正多角形(3次元) 星型多角形(2次元) 星型多角形(…
slpr.sakura.ne.jp
2次元平面上でxをpc(t)、yをps(t)と定義すると、3次元空間におけるxyz座標は以下のようになります。
$$ x = {\rm ps}(u)\cdot {\rm pc}(v) \\ y = {\rm ps}(u)\cdot {\rm ps}(v) \\ z = {\rm pc}(u) $$ここでは、媒介変数として$$0\le u \lt \pi, \;\; 0\le v \lt 2\pi$$の範囲を使用しています。
「z[z <= 0.02] = np.nan」というコードを使用することで、z座標が0.02以下の部分の図形を非表示にできます。この手法は以下の例でも活用しています。
[matplotlib 3D] 41. 円錐台(Truncated cone)
matplotlib mplot3dにより円錐台を表示する。
sabopy.com
2018.12.07
軸ラベルの設定
ax.set_box_aspect((1,1,1))により３Dグラフのアスペクト比を揃えています。
3Dグラフの表示
color=’gold’で金色、alpha=0.5で透明度0.5の図形が描写される。
コードをダウンロード(.pyファイル) コードをダウンロード(.ipynbファイル)参考
ピラミッド - Wikipedia
ja.wikipedia.org
正多角形とスピログラフの数式
正多角形とスピログラフの数式です。 正多角形(2次元) 正多角形(3次元) 星型多角形(2次元) 星型多角形(…
slpr.sakura.ne.jp
コメント