はじめに
matplotlibのFuncAnimationを使って、自由落下と反発係数を考慮したバウンドするボールのアニメーションを作成する方法を解説します。物理シミュレーションの基本原理から実装方法まで段階的に説明していきます。
コード
解説
モジュールのインポートなど
バージョン
時間データの作成
np.arangeを使用して0秒から15秒までの時間データを0.05秒間隔で作成します。これにより配列サイズは300になります。計算では重力加速度を9.8 m/s²としています。
自由落下時の位置変化
初期位置を100とした場合、地面に到着する時間はt_posi0になります。
この地面到達時間に対応するtのインデックスを求める必要があります。
これはnp.argmin(np.abs(t-t_posi0))という関数で計算できます。
自由落下の位置変化を表示すると以下のようになります。
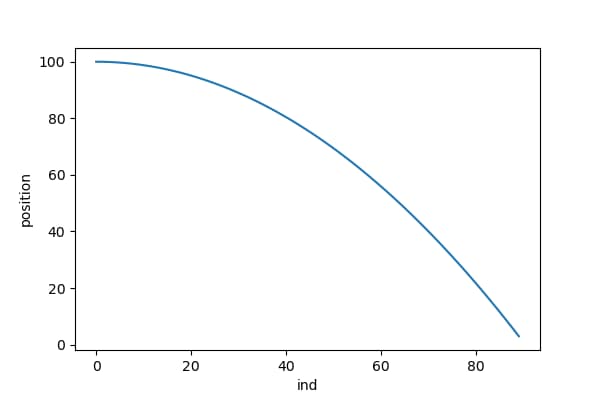
バウンド時の位置変化
反発係数を0.8と設定し、ボールの衝突前後のスピードを計算します。これにより、位置の変化は次のようになります。
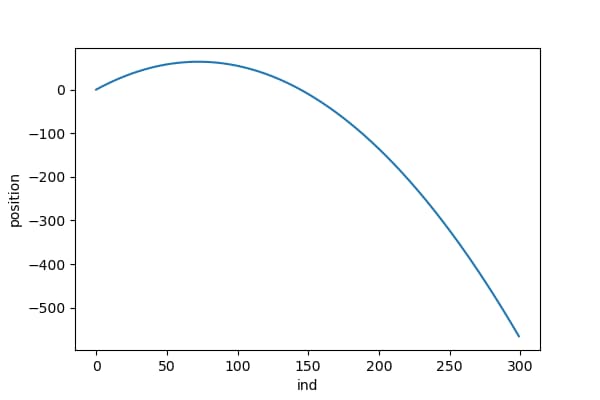
np.where(b1_z>0)[0][-1]を使用して位置が正の値である最後のインデックスを特定し、そのインデックスで位置データをスライスして表示すると次のようになる。
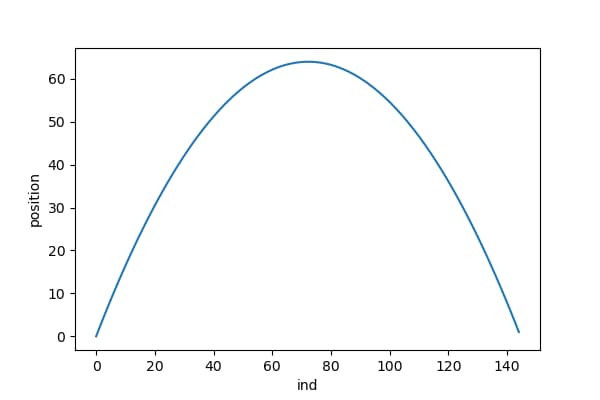
2回目のバウンド

3回目のバウンド
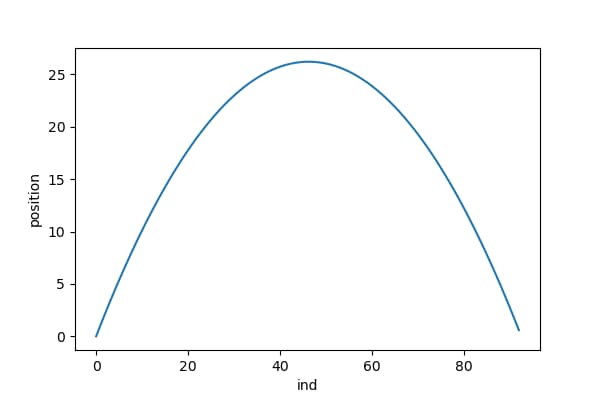
4回目のバウンド
5回目のバウンド
6回目のバウンド

位置データの連結
np.concatenate()関数を使用して全ての位置データを一つの配列に連結します。図示すると以下のようになります。

アニメーションで表示
ax.hlines(0,-.25,.25)を使用してy=0の位置に水平線を表示します。また、ax.spines[‘right’].set_visible(False)などの命令で右側、上側、下側の軸を非表示にし、左側の軸のみを表示します。
アニメーション関数の設定
set_ydataメソッドを使用して、plot関数で生成したball1オブジェクトのy軸データを更新します。
アニメーションの表示
FuncAnimationを使用してアニメーションを表示します。フレーム数は627、インターバルは10msに設定し、約6秒のアニメーションを作成します。
HTML(ani.to_html5_video())を実行することで、Jupyter NotebookやJupyter Lab上で直接アニメーションを表示できます。
また、ani.save(‘ファイル名’, writer=”ffmpeg”, dpi=100)を使用すると、アニメーションをMP4形式で保存できます。
反発係数を0.5とした場合
反発係数を0.95とした場合
まとめ
本記事では、matplotlibのFuncAnimationを用いてバウンドするボールのアニメーションを実装する方法を解説しました。重力による自由落下と反発係数を考慮したモデルにより、リアルな物理シミュレーションを実現できます。この手法は他の物理シミュレーションにも応用可能で、Pythonによる視覚化の可能性を広げるでしょう。
参考




コメント