[NumPy] 7. ブロードキャスト

NumPyによるブロードキャスト

ブロードキャストとは、形状の異なる配列間で算術演算を行うための NumPy の機能です。この機能により、小さい配列が自動的に大きい配列のサイズに拡張されるため、明示的なループを書かずに効率的な計算が可能になります。

1次元配列のブロードキャスト

配列の形状が同じ場合

ブロードキャストでは、配列の各要素に対して効率的に計算が実行されます。

ボクセルグラフによる視覚化

上記の計算をボクセルグラフで図示すると下記のようになります。

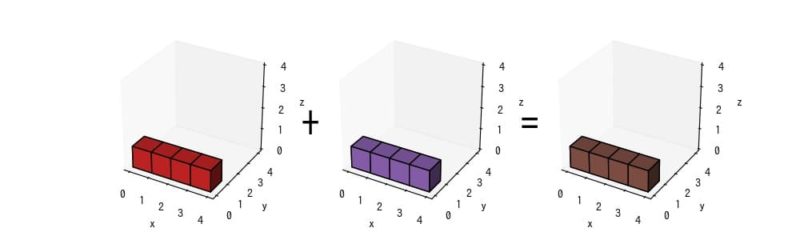
配列の形状が異なる場合

ブロードキャスト機能により、配列aの各要素に値2が自動的に加算されます。

ボクセルグラフによる視覚化

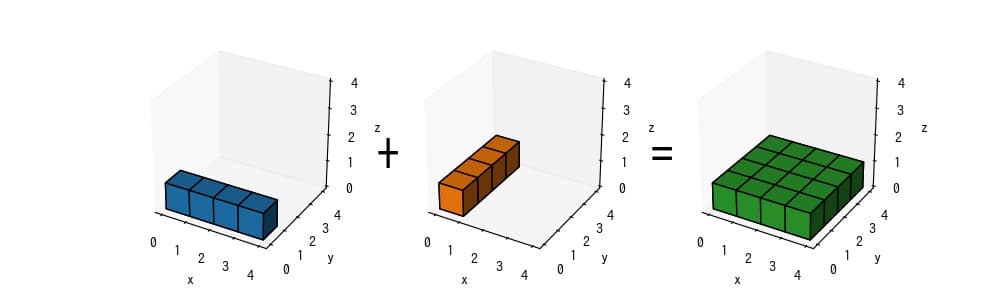
上記の計算をボクセルグラフで視覚化すると、以下のような図になります。

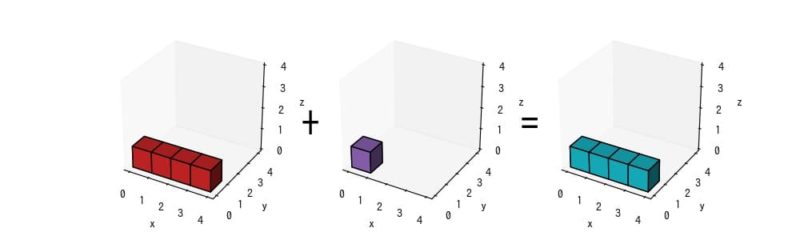
2次元配列のブロードキャスト

2次元配列に1次元配列をブロードキャスト

np.ones()で3×4の要素がすべて1の配列を作成します。

この配列にa=[0., 1., 2., 3.]を足すと、ブロードキャストによりすべての行に対してaの値が加算されます。

同様に、a*cの計算では、cのすべての行に対してaの値が乗算されます。

ブロードキャストで2次元配列を生成

dはaの配列の形状をnp.newaxisによって(4,1)に変換したものです。

このdをa_と足し合わせると、a_の配列の形状は(1,4)であるため、ブロードキャストが適用され、生成される配列の形状は(4, 1) × (1, 4) = (4, 4)となります。

ここでは理解しやすいようにa_= a[np.newaxis]で次元を増加させていますが、実際にはaでも計算時に自動的に形状が(4,)から(1,4)に変換されるため、同様にブロードキャストが可能です。

ボクセルグラフによる視覚化

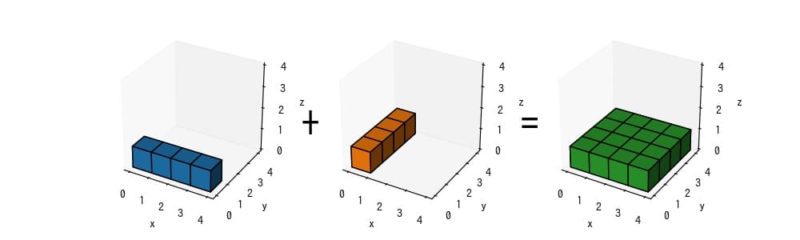
3次元配列のブロードキャスト

ブロードキャストで3次元配列を生成

fはaを3次元化した配列であり、形状は(4, 1, 1)です。これを形状が(1, 4, 4)であるeとブロードキャストで計算すると、(4, 1, 1) × (1, 4, 4) = (4, 4, 4)の配列が生成されます。

ボクセルグラフによる視覚化

コードをダウンロード(.pyファイル)

コードをダウンロード(.ipynbファイル)

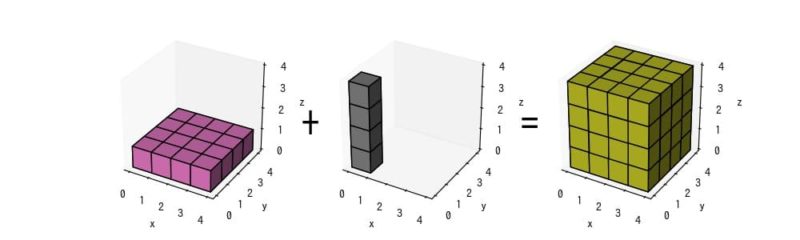
参考

NumPyのブロードキャストのメリットと解説

NumPyには演算を行う際に配列の形状(shape)を適切に調整するブロードキャスト(broadcasting)機能が備わっています。本記事では、ブロードキャストについての解説をします。

deepage.net

[matplotlib 3D] 28. Pythonで3D voxelグラフ

Pythonのmatplotlibを使用した3D voxelグラフの作成方法について解説します。voxelは3次元空間内のピクセルで、データの可視化や3D構造の表現に役立ちます。このチュートリアルでは基本的な使い方から応用例まで紹介します。

sabopy.com

2018.10.29