[scikit-learn] 12. GaussianMixtureモデルによるクラスタリング

はじめに

GaussianMixtureは、データが複数のガウス分布の混合から生成されていると仮定するモデルです。各ガウス分布はクラスターに対応し、その分布パラメータと混合比率を推定することでクラスタリングを行います。ここでは、ガウス分布に従う2つのデータセットに対するクラスタリング例と対数尤度の可視化方法を紹介します。

解説

モジュールのインポートなど

バージョン

データの生成

中心 (5, 0) の等方的ガウス分布に従うデータと中心 (-5, 0) の横に伸びたガウス分布に従うデータをそれぞれ300個、200個作成する。

2つのデータをnp.vstack()で結合します。

Gaussian Mixture Modelの定義とトレーニング

Gaussian Mixture Modelを2成分で定義します。成分数はn_components=2で指定し、共分散パラメーターのタイプはcovariance_typeで選択します。この例では”full”を使用しています。その他のオプションとして‘tied’, ‘diag’, ‘spherical’があります。

clf.fit(X_train)でトレーニングします。

データの分類

clf.predict(X_train)でデータを分類することができます。

等高線用データの作成

np.meshgridを使って等高線表示用の2次元グリッドデータを作成し、-clf.score_samples(XX)を適用することで各グリッドポイントにおける対数確率値をz軸データとして取得します。

結果の表示

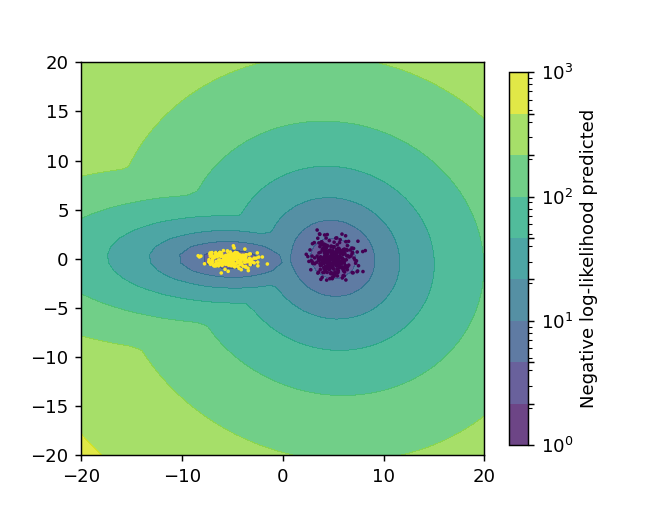
ax.scatter(X_train[:, 0], X_train[:, 1], s=1, c=labels)を使用すると、クラスター成分ごとに異なる色で散布図を表示できます。

モデルから得られるデータ

mean_

各成分の平均の値が得られます。

weights_

各成分の分率が得られます。

covariances_

各成分の共分散パラメータが得られます。

コードをダウンロード(.pyファイル)

コードをダウンロード(.ipynbファイル)

実践上の注意点

• 初期値の影響: 結果が初期値に依存するため、複数回の試行が推奨されます
• クラスター数の選定: BIC（ベイズ情報量基準）やAIC（赤池情報量基準）を使用して最適なクラスター数を決定できます
• 高次元データ: 次元の呪いに注意し、必要に応じて次元削減を検討します
• 外れ値の影響: 外れ値に敏感なため、前処理での対応が重要です

参考

GaussianMixture

Gallery examples: Comparing different clustering algorithms on toy datasets Demonstration of k-means assumptions Gaussia...

scikit-learn

Density Estimation for a Gaussian mixture

Plot the density estimation of a mixture of two Gaussians. Data is generated from two Gaussians with different centers a...

scikit-learn