はじめに
scikit-learnのlinear_model.Ridgeを使用したL2正則化について解説します。L2正則化は線形回帰モデルの過学習を抑制するための手法で、正則化パラメータalphaの調整によってモデルの複雑さをコントロールします。記事ではノイズの多いデータに対してalphaを変化させた際の効果をアニメーションで視覚的に示しています。
解説
モジュールのインポートなど
バージョン
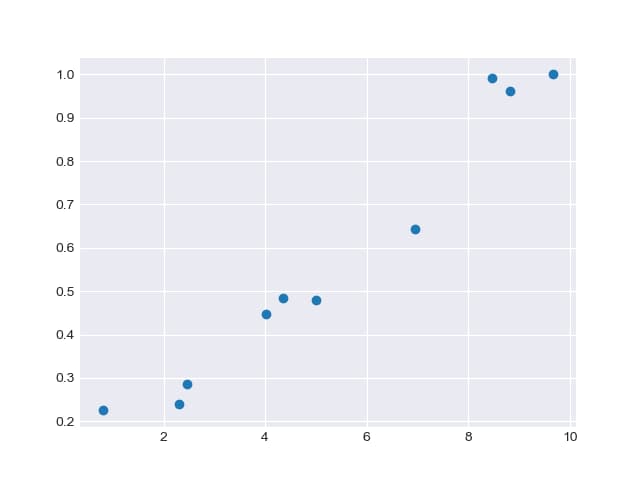
データの生成
10個のランダムな値(0-10の範囲)をxとして生成し、func(x)関数を使用してランダムなエラーを含む線形データを作成します。
データを表示すると以下のようになります。
PolynomialFeaturesによる多項式の設定
7次の多項式をdegree=7で定義します。その後、fit_transformを使用してx値を計算処理可能な形式に変換します。
予測に用いるxの設定
滑らかな予測結果を得るために、細かい間隔でxデータを作成します。
ridge回帰
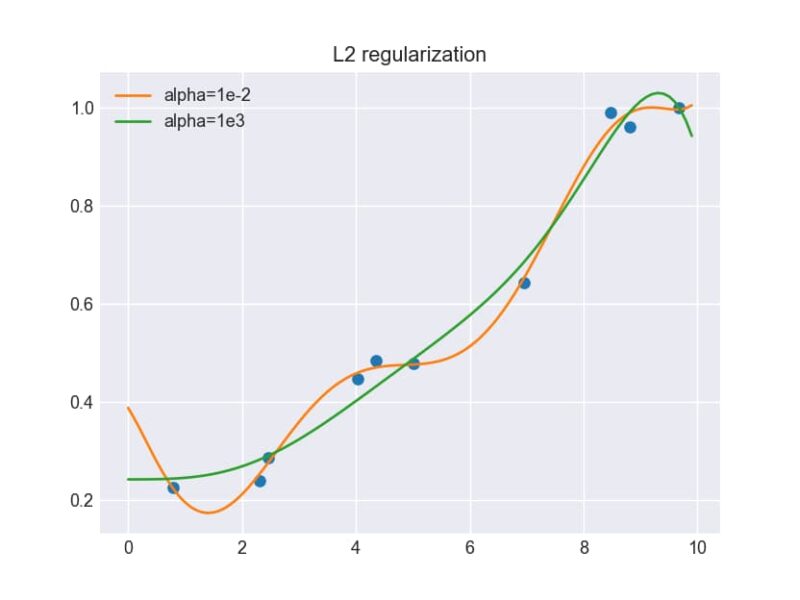
まず、Ridge(alpha=1e-2)で正則化パラメータαを0.01に設定します。次にfit(X_po, y)でモデルを学習させ、predict(xx_)で新しいデータに対する予測を行います。
この実験では、αの値を1e-2(0.01)と1e3(1000)の2通りで計算し、それぞれの予測結果を比較しました。
結果は明確な違いを示しています。αが1e-2の小さい値の場合、モデルはデータに過剰に適合してうねりが生じます。一方、αが1e3の大きい値の場合は、データへの過剰な適合が抑制され、より滑らかな予測曲線が得られます。
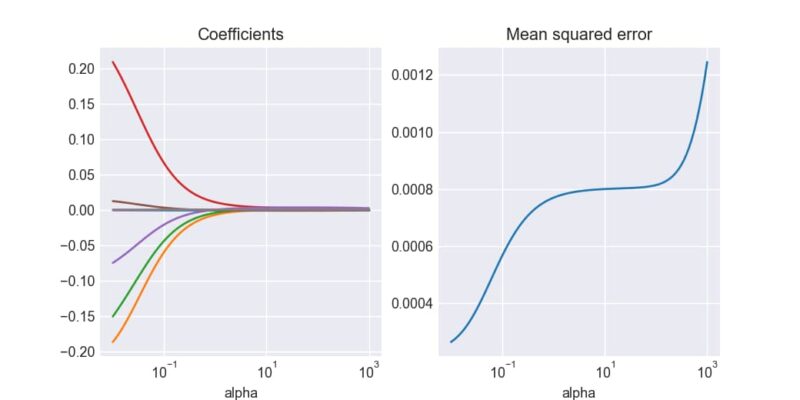
αを変えてデータを取得
正則化パラメータalphaを1e-2から1e3まで段階的に変化させ、各値における予測結果、係数の値、平均二乗誤差を取得します。
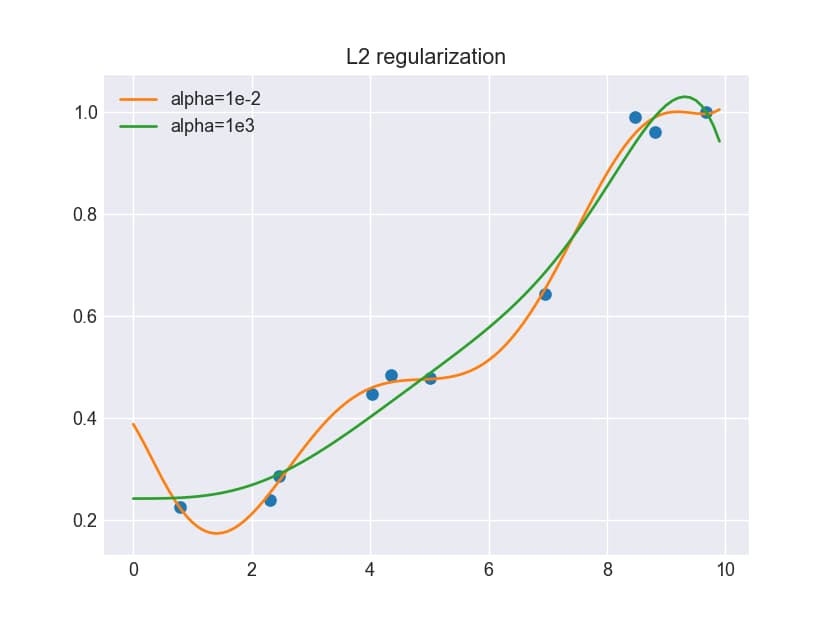
アニメーションで表示
正則化パラメータαの値を変えると、予測結果がどのように変化するかを以下のアニメーションで示します。
係数と平均二乗誤差の変化
αの値が大きくなるにつれて、係数は0に近づき、同時に平均二乗誤差が増加していくことが観察できます。
まとめ
- Ridge回帰は線形回帰にL2正則化項を追加して過学習を防ぐ手法
- 正則化パラメータ
alphaが大きいほど、モデルは単純になり過学習が抑制される alphaが小さいと、通常の線形回帰に近づきデータに過剰適合する傾向がある- scikit-learnの
Ridgeクラスを使うことで簡単に実装可能 - 最適な
alpha値は交差検証などを用いて決定するのが一般的
L2正則化は特に特徴量が多い場合や、特徴量間に相関がある場合に効果的です。適切なαの選択により、モデルの汎化性能を向上させることができます。

コメント