はじめに
この記事では、lmfitライブラリを使用して非線形最小二乗法によるカーブフィッティングを行う際に、フィッティングパラメータに代数的な制約を付与する方法について説明します。lmfitはScipy.optimize.curve_fitの拡張版であり、より柔軟なパラメータ設定が可能になっています。
コード
解説
モジュールのインポートなど
バージョン
残差を返す関数の定義
2つのガウス関数を組み合わせたmodelを作成し、return文でmodel – dataとして残差を返す関数を作成します。
ガウス分布データの生成
異なる分布を示すガウス分布を足し合わせたデータを作成します。
パラメータの設定
lmfitでは、Parameters オブジェクトを使用してフィッティングパラメータを定義し、それらに代数的な制約を設定することができます。
pfit = Parameters() として辞書形式のパラメータを作成して、そこに.add していくことでパラメータを追加していきます。変数peak_splitでvalue=2.5, min=0, max=5, vary=Trueとすることで初期値2.5で0から5まで変動するパラメータを作って、pfit.add(name='cen_2', expr='peak_split+cen_1')とすることでcen_2をcen_1からcen_1+5の範囲になるようにすることができます。
カーブフィット
Minimizer(residual, pfit, fcn_args=(x, data))により、残差を返す関数residualが最小となるようにパラメータを最適化する処理をします。mini.leastsq()で最適化が行われ、out.residualで残差を得ることができます。data + out.residualとすることでフィットしたカーブのデータを得ることができます。フィッティング後のパラメータの値は以下のようになります。
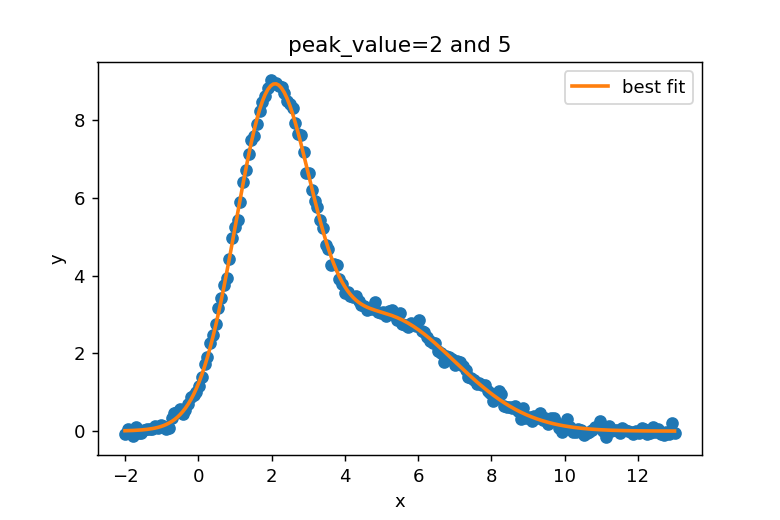
フィッティング結果の表示

代数的制約のためカーブフィットできていない事例
データにおいて、ピーク位置が2と7.5で差が5.5となっている場合、代数的な制約では大きい方のピークが7までしか位置できないため、フィッティング結果が不十分になります。

まとめ
lmfitは、パラメータに代数的な制約を付与することで、物理的・化学的な意味を持つモデルフィッティングを効率的に行うことができます。このような制約は、複雑な関係を持つパラメータの推定や、理論モデルに基づくデータ解析において非常に有用です。
代数的制約を活用することで:
- 物理的に意味のあるパラメータ関係を保持できる
- フィッティングの安定性が向上する
- パラメータの数を減らし、過学習を防ぐことができる
- 複雑なモデルでも直感的にパラメータ間の関係を定義できる
lmfitは科学研究やデータ解析において強力なツールであり、Scipyの基本機能を超えた柔軟なカーブフィッティングを可能にします。

コメント