[lmfit] 3. パラメータに代数的な制約を付与してカーブフィッティング

はじめに
コード
解説
参考

はじめに

lmfitは非線形最小二乗法を用いてカーブフィットするためのライブラリであり、Scipy.optimize.curve_fitの拡張版に位置する。ここでは、フィッティングパラメータに代数的な制約を付与してカーブフィッティングする方法について説明する。

コード

解説

モジュールのインポートなど

バージョン

残差を返す関数の定義

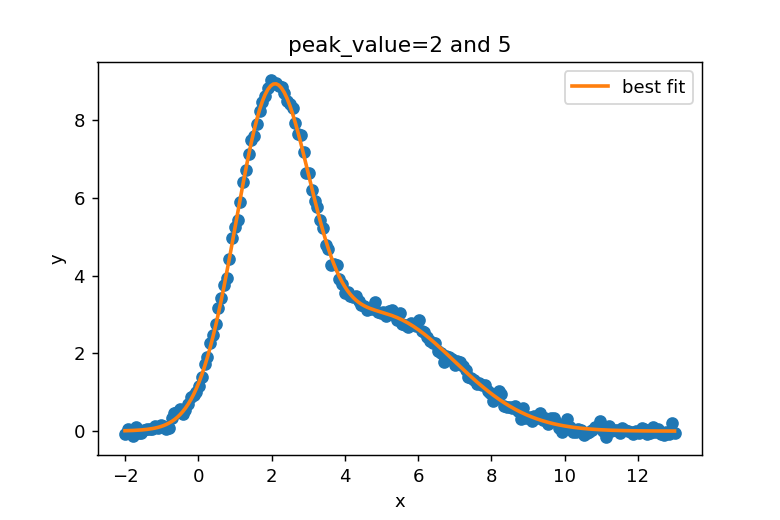
2つのガウス関数が重なったmodelを作成して、returnでmodel - dataとして残差を返す関数を作成する。

ガウス分布データの生成

異なる分布を示すガウス分布を足し合わせたデータを作成する。

パラメータの設定

pfit = Parameters() として辞書形式のパラメータを作成して、そこに.add していくことでパラメータを追加していく。変数peak_splitでvalue=2.5, min=0, max=5, vary=Trueとすることで初期値2.5で0から5まで変動するパラメータを作って、pfit.add(name='cen_2', expr='peak_split+cen_1')とすることでcen_2をcen_1からcen_1+5の範囲になるようにすることができる。

カーブフィット

Minimizer(residual, pfit, fcn_args=(x, data))により、残差を返す関数residualが最小となるようにパラメータを最適化する処理をする。mini.leastsq()で最適化が行われ、out.residualで残差を得ることができる。data + out.residualとすることでフィットしたカーブのデータを得ることができる。

フィッティング後のパラメータの値は以下のようになる。