はじめに
データ分析やモデリングにおいて、実験データから適切な曲線を見つけることは非常に重要です。Pythonのscipy.optimizeモジュールに含まれるcurve_fit関数を使えば、簡単に最小2乗法による曲線フィッティングが行えます。
curve_fit関数は以下のような特徴があります:
- 任意の関数モデルに対応可能
- パラメータの初期値を指定できる
- パラメータの範囲を制限できる
- フィッティングの不確かさも計算できる
これらの特徴により、実験データの解析や物理モデルのパラメータ推定など、様々な場面で活用できます。
コード
解説
モジュールのインポート
バージョン
データの生成
np.linespaceは(-1,1,20)の場合、-1から1までの範囲で均等に分布した20個の値からなる配列を生成します。
np.random.rand(1)は0〜1の範囲で乱数を1個生成します。この例では、1次関数の係数をこのランダム値で設定しています。
np.random.normal()は標準正規分布に従う乱数を生成します。sizeパラメータにlen(x_data)を指定することで、x_dataと同じ長さ(20個)の乱数配列を生成しています。[1]
近似式を定義
近似に用いる関数を定義します。[2]
curve_fitで近似
関数funcを用いてx_dataとy_data_1をフィッティングします。poptは最適推定値となり、np.random.rand()で生成した値に近似します。pcovは共分散行列を表します。[3]
R2の計算
決定係数(r_squared)は1に近いほど、その近似の信頼性が高いことを示します。
residualsはデータと近似曲線の差(残差)を表しています。
rssはresidual sum of squaresの略で残差の2乗の合計、tssはtotal sum of squaresの略で各y_dataとy_dataの平均との差の2乗の合計であり、データそのもののばらつきを表します。[4]
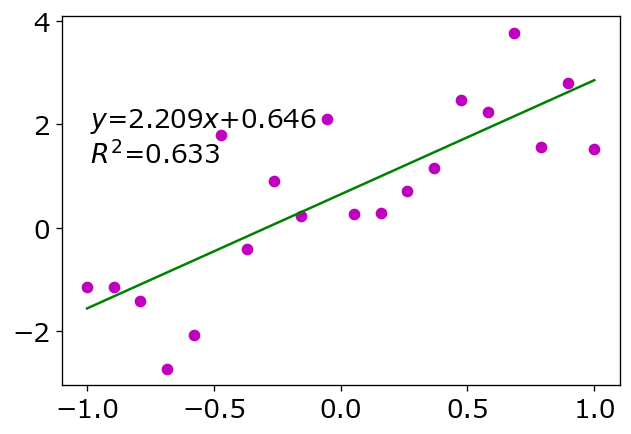
dataを点, 近似結果を線でプロット
‘mo’はマゼンダ(m)の丸(o)でプロットすることを意味し、’g-‘はグリーン(g)の線(-)でプロットすることを意味します。
この表記法で使用できる色は{'b', 'g', 'r', 'c', 'm', 'y', 'k', 'w'}(青、緑、赤、シアン、マゼンダ、黄、黒、白)に限定されています。[5]
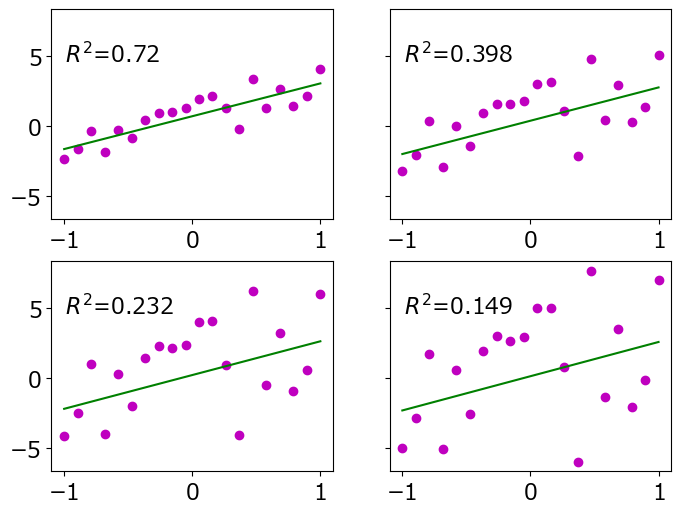
誤差を大きくした時の近似結果の変化
このグラフでは、エラー値を2倍、3倍、4倍に増加させた場合のフィッティング結果の変化を観察しました。
結果は以下の通りです。左上がエラー1倍、右上がエラー2倍、左下がエラー3倍、右下がエラー4倍の場合の結果を示しています。誤差の増加に伴いR²値が低下していることから、R²が正しく計算されていることが確認できます。

コメント