はじめに
lmfitは、Python環境で非線形最小二乗法によるカーブフィッティングを行うための強力なライブラリです。SciPyのcurve_fit関数を拡張し、より柔軟なパラメータ管理や制約の設定、様々な組み込みモデルを提供しています。ここでは、lmfitでデータをsin関数モデルによりカーブフィッティングする方法について説明します。
sin関数モデルの基本
正弦波モデルは周期的な振る舞いを示すデータの解析に適しています。一般的なsin関数モデルは以下の形式で表されます:
y = amp * sin(freq * x + phase) + offset
ここで:
- amp: 振幅(波の高さ)
- freq: 周波数(波の密度)
- phase: 位相(波のシフト)
- offset: オフセット(基準線からの距離)
コード

解説
モジュールのインポートなど
バージョン
データの生成
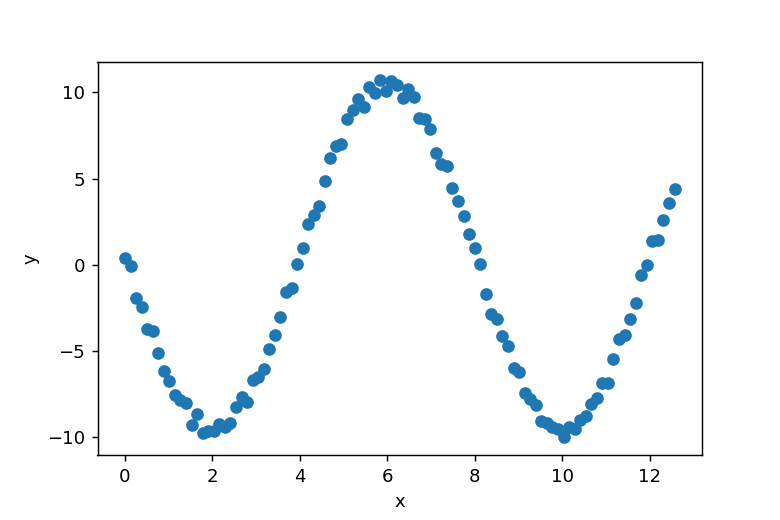
テストデータは関数f(x,a,f,p)を用いて生成します。NumPyのdefault_rng()を使用し、rng.random(100)によりランダムなノイズを作成してyデータに加えます。以下のグラフはxとyの関係を示しています。
モデルの定義
lmfit.models の SineModelをモデル関数として用います。
初期パタメータの推定
model.guess(y, x=x)を使用して、上図のデータをsin関数モデルで近似するためのフィッティングパラメータの初期値を推定します。これにより得られるパラメータ(params)は以下のようになります。
カーブフィット
model.fit(y, params, x=x)により、カーブフィッティングを実行します。
フィッティング結果の表示
print(result.fit_report())により、フィッティングの結果を見ることができます。
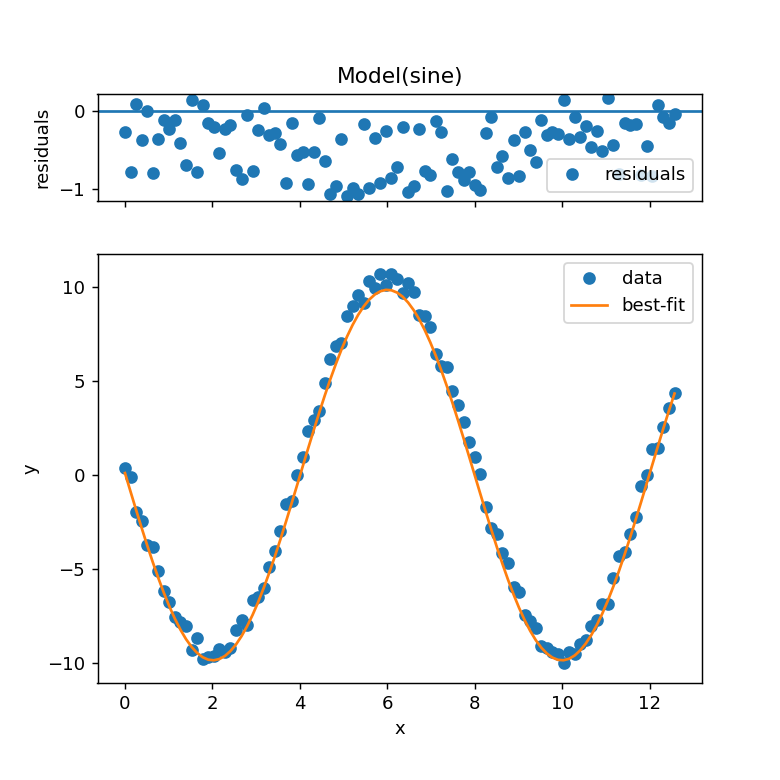
result.plot_fit()によりデータとフィッティングカーブが表示されます。

result.plot()を実行すると、フィッティング結果とともに残差が表示されます。
まとめ
lmfitを使用したsin関数モデルによるカーブフィッティングは、周期的な現象を分析する際に非常に有用です。このアプローチは、信号処理、時系列解析、物理実験データの解析など様々な分野で応用できます。パラメータの適切な初期値設定と制約の活用が、精度の高い結果を得るための鍵となります。
さらに詳しく知りたい方は、lmfitの公式ドキュメントや、様々なモデルの組み合わせについて探求してみることをお勧めします。

コメント