はじめに
本記事では、Pythonのmatplotlibライブラリを使用して1次元拡散方程式による熱拡散のアニメーションを作成する方法を解説します。FuncAnimationを活用して時間経過に伴う熱の拡散過程を視覚的に表現する手法を紹介します。
解説
モジュールのインポート
バージョン
定数の設定
1次元の棒における拡散方程式の解は以下のようになります。
ここで、Hはx=0に印加する熱エネルギー、Cpは比熱容量、Aは棒の断面積です。Dは熱拡散率、xは棒の位置、tは時間を表します。
\[\theta(x,t) = \frac{H}{c_pA}\frac{1}{\sqrt{Dt}}\frac{1}{\sqrt{4\pi}}\exp\left(-\frac{x^2}{4Dt}\right)\]
これらの定数を以下のように定義します。
棒の長さの設定
棒は-0.05 m から0.05 mの範囲を表示します。
時間の設定
まずは、時間 (0.001, 0.01, 0.1) における温度分布を可視化してみましょう。
結果の表示
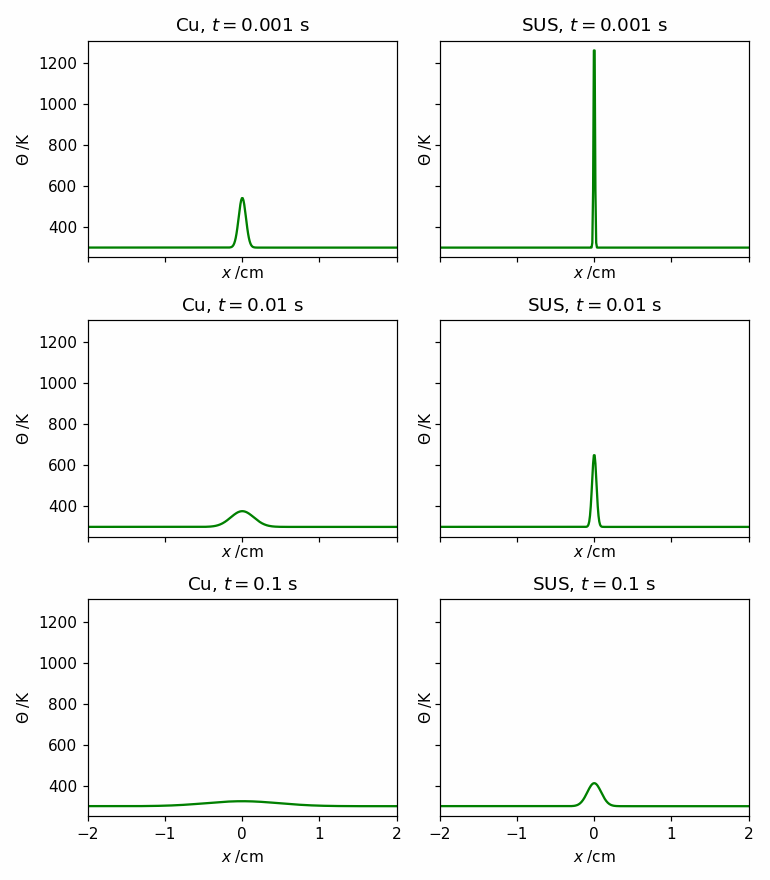
銅とステンレスの各時間における温度分布を以下に示します。
なお、sharex=True、sharey=Trueを設定することで、x軸とy軸の表示範囲を統一しています。
Cuの熱拡散アニメーション
データの生成
np.logspace(-3,0,200)を使用して対数スケールの時間配列を設定し、各時間における解を計算してリストに追加します。
アニメーション関数の設定
cu, = ax.plot(x*100, thetas[0], ‘C1-‘) でプロットを作成し、cu.set_ydata(thetas[num])によりyデータを更新することでアニメーションを生成します。
アニメーションの表示
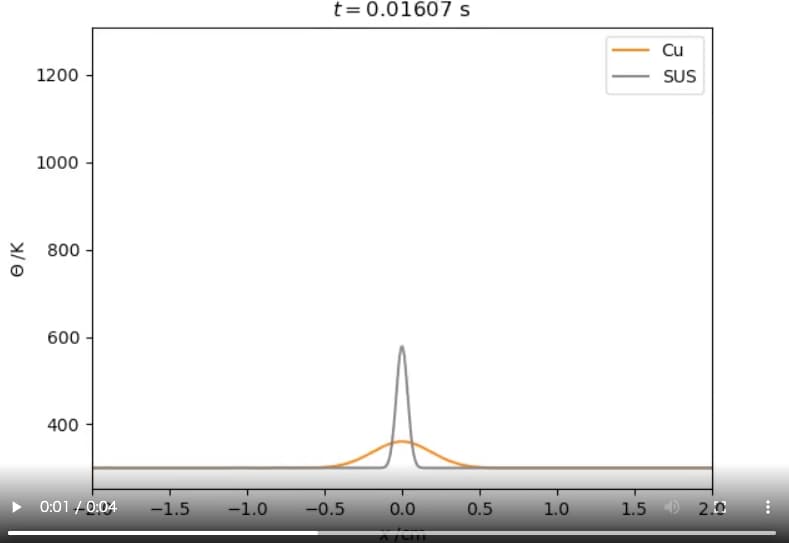
CuとSUSの熱拡散アニメーション
CuとSUSの結果を同時に表示すると以下のようになります。
まとめ
本記事では、matplotlibのFuncAnimationを使用して1次元拡散方程式による熱拡散のアニメーションを作成する方法を解説しました。Pythonで物理現象をシミュレーションし視覚化することで、複雑な現象への理解が深まります。このテクニックは他の偏微分方程式のシミュレーションにも応用可能です。

コメント