[matplotlib animation] 14. 外サイクロイド(epicycloid)

はじめに
コード
解説
まとめ
参考

はじめに

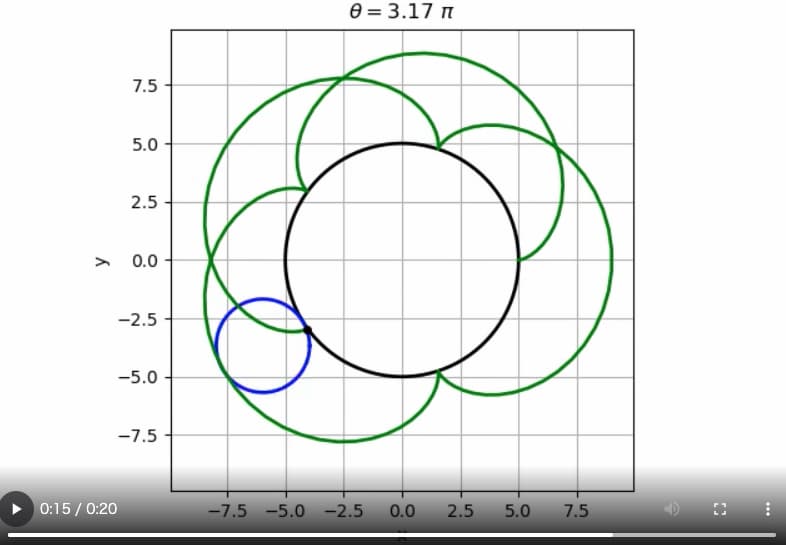
本記事では、matplotlibのFuncAnimationを使用して外サイクロイド（epicycloid）のアニメーションを作成する方法を解説します。外サイクロイドは、ある円が別の円の外側を転がるときに、円周上の点が描く軌跡です。

コード

解説

モジュールのインポート

グリッドと軸ラベル、アスペクト比の設定

データの生成

外サイクロイドは極座標系の媒介変数を用いてデータを生成します。この際、θは0〜4π、φは0〜2πの範囲で設定します。

外サイクロイド

中心円の半径をrc、動円の半径をrm、回転角をθとすると、外サイクロイドは以下の式で表されます。

$$x=(r_c + r_m)cos\theta -r_m cos( \frac{r_c + r_m}{r_m}\theta)\\ y=(r_c + r_m)sin\theta -r_m sin( \frac{r_c + r_m}{r_m}\theta)$$

外サイクロイドを表示するための空のリスト「epicycloids = []」を作成します。また、「points」は円周上の定点を表示するための空のリストです。

動く円

回転する円をプロットするために、極座標表示（x, y）で円を設定します。円をアニメーション表示するために、空のリスト「round_circles = []」を作成します。

円を移動させるための変数を設定します。動円は半径が(rm+rc)の円運動をするため、このような計算になります。

中心円

中心円は動かないため、アニメーション開始前にここでプロットしておきます。

アニメーションの設定

アニメーションでは古いプロットを消す必要があるため、グラフのリストに要素がある場合はpop().remove()メソッドで削除します。

round_circle, = plt.plot(x_move[num]+xm, y_move[num]+ym, ‘b-‘, lw=2)のコードで、外側の円を円運動するアニメーションとして表示します。’b-‘パラメータにより青い線で描画されます。

epicycloid, = plt.plot(x[:num+1] ,y[:num+1], ‘g-‘, lw=2)で、外サイクロイドの軌跡を表示します。’g-‘パラメータにより緑の線で描画されます。

point, = plt.plot(x[num], y[num], ‘ko’, markersize=4)で、外側の円上の定点（サイクロイドを描く点）を表示します。’ko’パラメータにより黒い丸で描画されます。

これらの作成したプロットを空のリストに追加することでアニメーションを実現できます。

ax.set_title(theta_str + str(theta[num]/np.pi)[:4] + str(r’ $\pi$’))でタイトルに変化する回転角を表示します。πを表示するには、r’ $\pi$’と記述します。

point, = plt.plot(x[num], y[num], ‘ko’, markersize=4)

でサイクロイドを描写する、外側の円上の定点を表示している。koで黒丸での表示となる。

それぞれ作成したプロットをからのリストに入れることでアニメーションを表示できる。

ax.set_title(theta_str + str(theta[num]/np.pi)[:4] + str(r’ $\pi$’))でタイトルにアニメーションで変化する回転角を表示する。πを表示するには、r’ $\pi$’とする。

アニメーションの表示

FuncAnimationを使用してアニメーションを表示します。updateを200ステップ実行してアニメーションを生成します。intervalは100msに設定されているため、アニメーションの総再生時間は20秒になります。Jupyter Notebook上では、HTML(ani.to_html5_video())を実行することでアニメーションを直接表示できます。