[SciPy] 2. ガウス分布によるカーブフィッティング

はじめに
コード
解説
まとめ
関連記事
参考

はじめに

SciPyライブラリのcurve_fit関数を使用して、測定データにガウス分布を当てはめる方法を解説します。ガウス分布（正規分布）は自然界の多くの現象を表現できるため、実験データの解析によく使われます。本記事では、ガウス関数の定義から始め、SciPyでのフィッティング方法、パラメータの解釈までを丁寧に説明していきます。

コード

解説

モジュールのインポート

バージョン

データの生成

norm.rvs(loc=100,scale=5,size=1000)

normは正規分布（ガウス分布）を表し、rvs（Random variates）関数でランダムな確率変数を生成できます。この例では、平均値100、標準偏差5の正規分布に従う確率変数を1000個生成しています。

hist_1, bins = np.histogram(sample_1, 100, range=(50,150)) np.histogram関数を使用してヒストグラムデータを取得できます。この関数は、ヒストグラムの度数（hist_1）と区間の境界値（bins）を返します。sample_1はヒストグラム化したいデータ、100は区間の数、rangeパラメータは値の範囲（50から150）を指定しています。

bins = bins[:-1] bins配列には区間の境界値が格納されるため、区間が100個の場合、境界値は101個になります。そのままplt.plot(bins,hist_1)でプロットすると、ValueError: operands could not be broadcast together with shapes (101,) (100,) というエラーが発生します。これを防ぐため、bins配列の最後の要素を削除しています。

フィッティングする関数の定義

$$\displaystyle f(x)=a \exp\left(-\frac{(x-\mu)^2}{2\sigma^2} \right)$$

ガウス分布関数を定義します。

カーブフィッティング

param_iniはフィッティングパラメータの初期値です。ガウス分布の関数の引数を3つ設定しているため、(強度、期待値、標準偏差)の順になります。

popt, pcov = curve_fit(func, bins, hist_1, p0=param_ini) この関数では、funcにフィッティングしたい関数、binsとhist_1にそれぞれx軸とy軸のデータ、p0にパラメータの初期値を指定します。実行結果として、poptにフィッティングで得られた最適パラメータ、pcovに共分散行列が返されます。

フィッティング結果のデータを生成するには、得られたパラメータpoptをガウス分布関数(func)に適用するだけで完了です。

近似曲線の図示

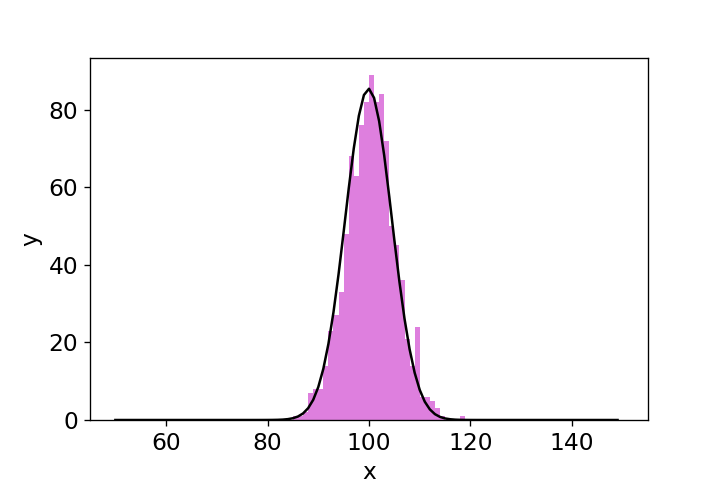
ax.bar(bins,hist_1,width=100/100,alpha=0.5,color='m',align='edge')でヒストグラムを表示します。widthは（ヒストグラムの範囲/binsの要素数）とすることで隙間なく表示できます。align='edge'パラメータは棒グラフの配置位置を制御します。デフォルトではx=50のとき棒のセンターがx=50に位置しますが、'edge'を指定すると棒の左端がx=50に位置するようになります。

ax.plot(bins,fitting,'k')を使用して、カーブフィッティングしたガウス分布を表示します。

コードをダウンロード(.pyファイル)

コードをダウンロード(.ipynbファイル)