はじめに
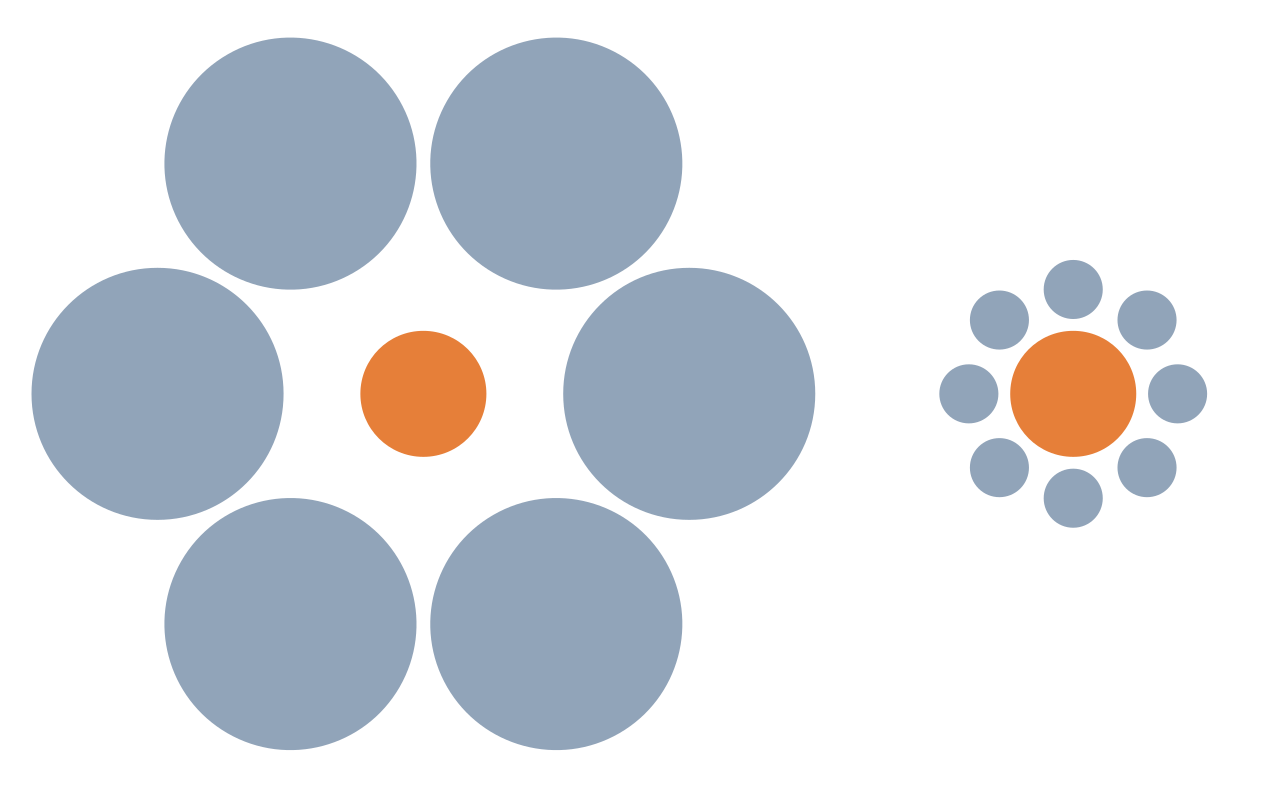
エビングハウス錯視は相対的な大きさに関する錯視の一種です。同じ大きさの円が大きな円と小さな円に囲まれている場合、大きな円に囲まれた円は小さく、小さな円に囲まれた円は大きく見えます。この記事では、このような視覚的錯覚をmatplotlibを使用してアニメーションで確認する方法を解説します。
コード
解説
最初に下記画像を作成する。

モジュールのインポート
左側の図の設定
データの生成
外側の円のデータを生成します。円の中心位置は媒介変数を用いて設定しています。
外側の円
xとyにはそれぞれ6つの値があり、各x,y座標でCircleオブジェクトを使って円を生成します。ax.add_patch(circle)を使用することで、これらの円を図に表示できます。
中心の円
中心の円は外側の円と同じ方法で挿入します。
右側の図の設定
右の図は左の図と同様に設定しています。外側の円は左のものより小さいですが、中心の円はCircle((1, 0), 0.15,color=’tab:orange’)で、左の図と同じ大きさです。
軸とアスペクト比の設定
ax.axis(‘off’)で軸を非表示にできます。
ax.axis(“equal”)を使うとアスペクト比が揃い、円が歪まずに表示されます。このアニメーションでは、左側の円群が右へ移動して再び戻る動きを表示します。
アニメーションに用いるパラメータ
外側の円の半径の設定
円の半径を0.3から0.1に段階的に小さくするために、np.linspace(0.3,0.1)で配列を作成します。np.linspaceで要素数を省略すると、デフォルトで要素数は50になります。
逆に0.1から0.3へと大きくするには、前述の配列に[::-1]を適用して逆順にします。これらをnp.hstackで結合することで、0.3から0.1へ小さくなった後、0.1から0.3へ大きくなる計100要素の配列が得られます。
外側の円の座標の設定
外側の円の座標を設定します。横方向の位置はx_l-1からx_r+1へ移動します。x_lが配列のため、linspaceで生成する配列は2次元配列になります。
円の半径変化と同様に、逆順の配列を結合します。この場合は2次元配列なのでvstackを使います。
縦方向の位置変化はy_lからy_rになるため、横方向の移動と同じ方法で作成します。
中心の円の座標の設定
中心の円の横方向の位置は-1から1へ移動するため、外側の円の座標と同じ方法で作成します。縦方向の位置は常に0のため、np.zerosを使って0の配列を生成します。
figの作成
最初に左側の円群を表示します。c1からc6は外側の円を、c_cは中心円を表します。
アニメーションの初期設定
アニメーションを機能させるには、return c1, c2, c3, c4, c5, c6, c_cのように、更新するすべての変数をreturn文に含める必要があります。
アニメーションの設定
円の位置はset_centerメソッドで設定し、円の半径はset_radiusメソッドで設定します。
このアニメーションでは中心円の半径が変化しているように見えますが、実際には中心円の半径は一定のままです。
init関数と同様に、アニメーション関数内でもreturn c1, c2, c3, c4, c5, c6, c_cのように更新するすべての変数をreturnする必要があります。
アニメーションの表示
animation.FuncAnimation()のinit_func=init,パラメータでinit関数を実行します。また、interval = 50, frames = 100を設定することで、50ミリ秒間隔の100フレームアニメーションが作成されます。
HTML(ani.to_html5_video())を使用すると、Jupyter NotebookやJupyter Labでアニメーションを簡単に表示できます。
中心円にそった水平線を表示した場合
中心円の大きさが変化していないことがわかります。
コードをダウンロード(.pyファイル) コードをダウンロード(.ipynbファイル)まとめ
エビングハウス錯視のアニメーションをmatplotlibで作成することで、同じ大きさの円が周囲の円のサイズによって異なる大きさに見える現象を動的に表現できます。これにより、人間の知覚システムがいかに周囲の環境に影響されるかを視覚的に理解することができます。
参考



コメント