はじめに
本記事では、ipywidgetsのFloatLogSliderを使用して、L2正則化(Ridge回帰)のパラメータ(alpha)を調整する方法について解説します。過学習を抑制するための正則化手法を、インタラクティブに調整できる方法を紹介します。
解説
モジュールのインポートなど
バージョン
データの生成
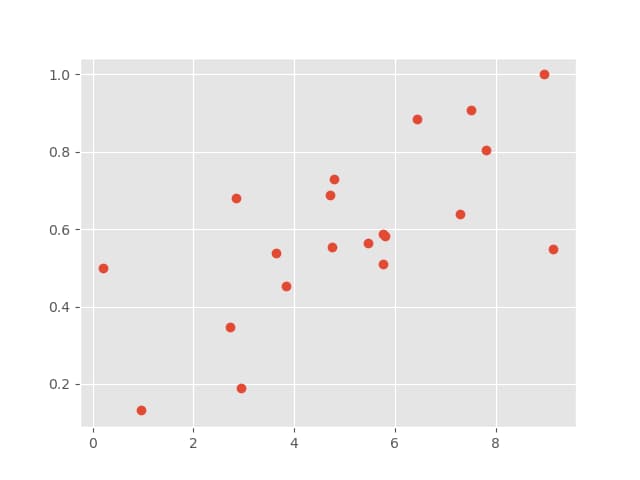
xを0から10の範囲でランダムに20個生成し、func(x)関数を用いてランダムなエラーを含む線形データを作成する。
データを表示すると以下のようになります。
PolynomialFeaturesによる多項式の設定
degree=7を指定して7次の多項式を定義します。fit_transformメソッドを使用することで、x値を計算処理に適した形式に変換します。
予測に用いるxの設定
滑らかな予測結果を得るため、細かい間隔でxデータを作成します。
ridge回帰
正則化パラメータαを0.01に設定するため、clf = Ridge(alpha=1e-2)を実行します。clf.fit(X_po, y)で学習を行い、y_ridge_em2 = clf.predict(xx_)で学習したモデルを使ってデータを予測します。
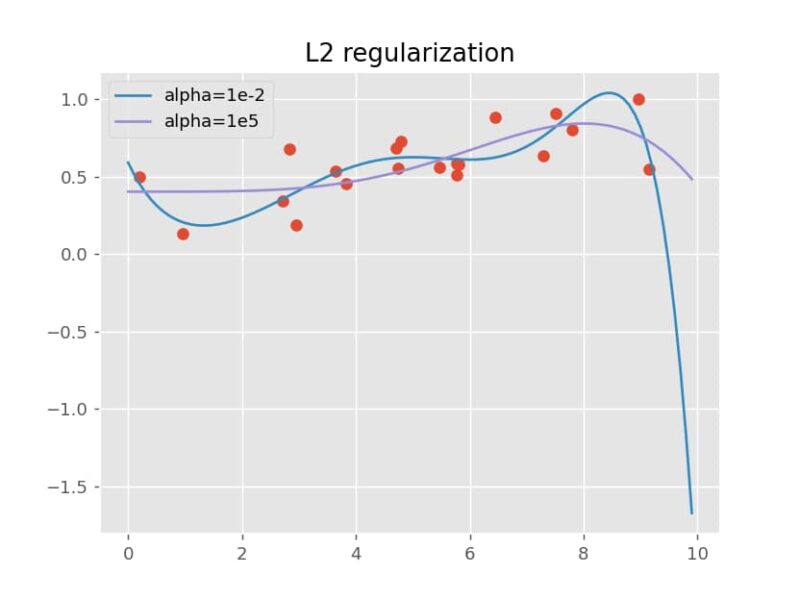
この例では、パラメータαを1e-2(0.01)と1e5(10万)の2つの値で計算し、それぞれの予測結果を比較しました。
結果は次のようになります。αが1e-2の小さい値の場合、モデルはデータに強く追従するためうねりが見られますが、αが1e5の大きい値の場合、データへの過度な追従が抑えられ、より滑らかな予測曲線が得られています。
FloatLogSliderでαを調整して結果を表示
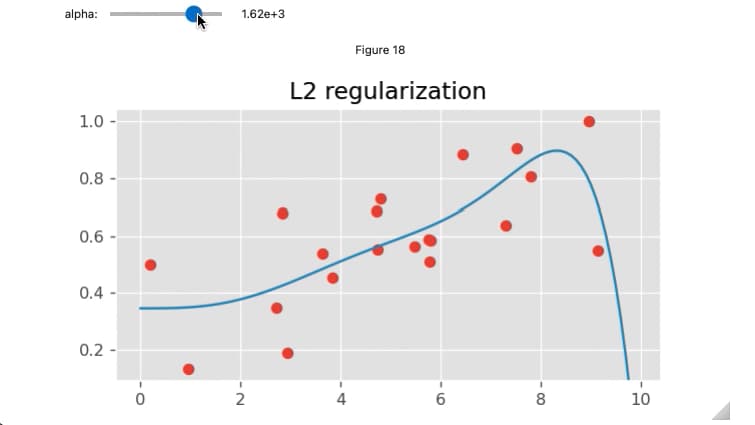
FloatLogSliderのスライダーを動かすことでαを調整し、そのalphaによる回帰結果をリアルタイムで表示します。これにより、正則化パラメータの変化に伴う予測結果を対話的に理解できるようになります。
係数と平均二乗誤差の変化
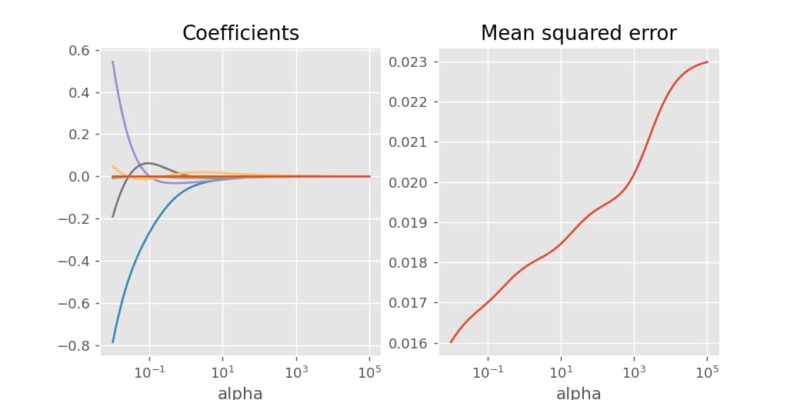
alphaの値を1e-2から1e5まで変化させると、係数の値と平均二乗誤差の変化を観察できます。結果から、αが大きくなるにつれて係数は0に近づき、平均二乗誤差は増加していくことがわかります。
まとめ
FloatLogSliderを使うことで、L2正則化のalphaパラメータを対数スケールで簡単に調整でき、過学習の抑制効果をリアルタイムで確認できます。これにより、モデルの汎化性能を向上させるための最適なパラメータを効率的に探索できます。

コメント