はじめに
lmfitライブラリを使用してデータをガウス関数モデルでカーブフィッティングする際に、basinhopping法を適用した実験について説明しています。様々なパラメータを変化させながらフィッティングを行い、iter_cb関数を用いてその過程のデータを取得。さらに、matplotlib FuncAnimationを使ってフィッティング過程をアニメーション化し、各パラメータがフィッティング結果に与える影響を視覚的に分析しています。
コード&解説
モジュールのインポート
バージョン
データの生成
lmfit.lineshapes モジュールの gaussian 関数を使用してガウス分布のラインプロファイルを作成します。また、np.random.random(len(x))/100 を用いてデータにノイズを追加します。
モデルとパラメータの設定
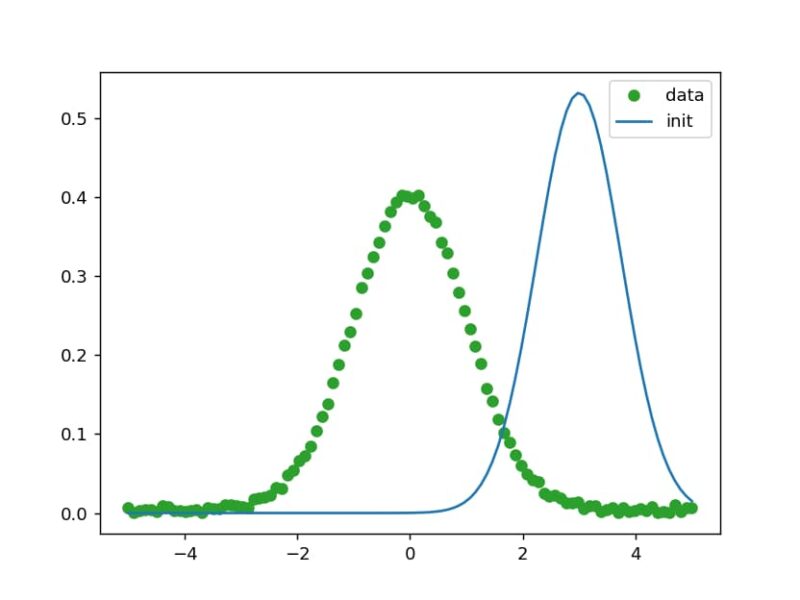
GaussianModel()を使ってガウス分布のモデルを作成し、model.make_params()でパラメータを生成します。パラメータの値はparams[“center”].set(value=3)のような形式で設定します。x値、y値、そして初期値を適用したモデルから得られるデータの関係は、以下の図のようになります。
コールバック関数の設定
この関数にはフィッティングの試行ごとに実行する処理を記述します。ここでは、valuesdict形式の辞書でパラメータをp_listに追加していく処理を実装しました。
フィッティングの実行
空のリストを作成し(p_list=[])、
model.fit(y, x=x, params=params, iter_cb=per_iteration, method=”basinhopping”, fit_kws=dict(niter=3))でコールバック関数を実行しながらフィッティングを行います。処理時間短縮のためniter=3に設定しています。
print(result.fit_report())を使用してフィッティング結果を表示できます。
カーブフィット結果の表示
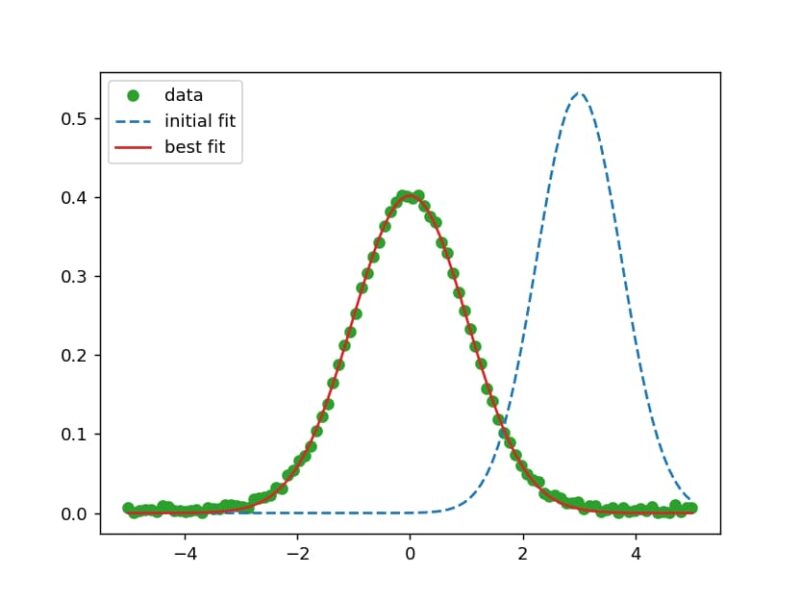
result.best_fitはフィッティング後のデータを表しています。図を見ると、モデルがデータに対して適切にフィッティングできていることが明確に分かります。
アニメーション
各パラメータでモデル曲線を再現し、リストに追加していく処理
パラメータリストから値を順番に取り出し、それぞれをモデルに適用して曲線を生成します。生成した曲線をリストに追加していき、最終的にnp.arrayに変換します。
アニメーションの表示
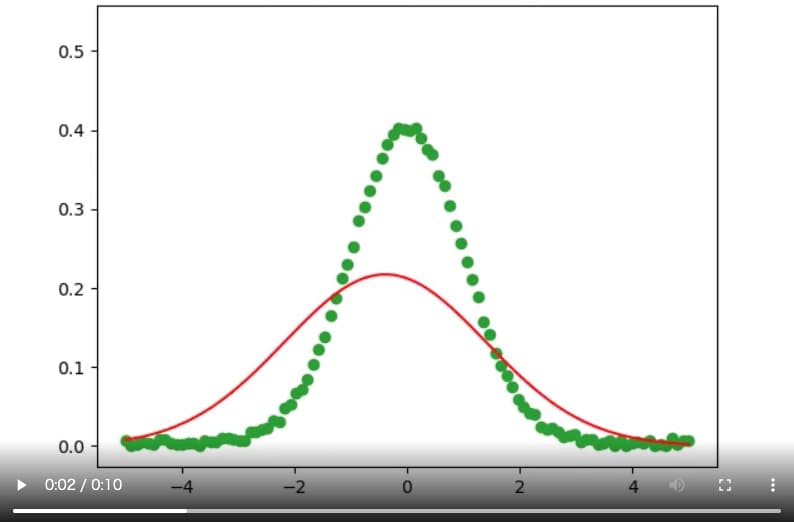
モデル曲線を更新するために、pを設定してp.set_ydataでfit_dataをプロットしていきます。以下にアニメーションを示します。このアニメーションでは、一度収束した後に再度初期値を設定し直してフィッティングを行う、basinhopping法の特徴的な挙動を観察できます。
step sizeを変化させた場合
stepsizeは初期値をランダムに変える際の最大ステップサイズです。この値が大きいほど初期値の移動量も大きくなります。デフォルト値は0.5ですが、下の動画では3に設定した結果を示しています。システムはデフォルトでも最適値を見つけるためにステップサイズを自動調整しますが、この過程には時間がかかることがあります。したがって、最適なステップサイズがあらかじめわかっていれば、フィッティング処理を高速化できると考えられます。
intervalを変化させた場合
intervalは、不適切な初期値の場合でも諦めずに反復する回数を設定できるパラメータと考えられます。デフォルト値は50ですが、下の動画では10に設定した時のフィッティングの様子を示しています。デフォルトの場合と比較すると、初期値がより活発に移動しているように見えます。
niterを変化させた場合
niterパラメータではbasinhoppingの反復回数を設定できます。デフォルト値は100で、かなり時間がかかります。niterを10に設定した場合、下図のように複数回のフィッティングが繰り返される過程を観察できます。fit_reportによるとfunction evalsは512となり、以前のniter=3の時(function evals = 216)と比較して、より多くの計算が実行されていることが分かります。
まとめ
basinhopping法は局所的な最小値に陥りやすい最適化問題において、より良い解を見つけるための効果的な手法です。今回の実験では、パラメータの変化がフィッティング精度にどう影響するかをアニメーションで可視化することで、最適なパラメータ設定への理解を深めることができました。特に初期値の設定や温度パラメータの調整が重要であることが確認されました。

コメント