[matplotlib] 44. triplotでドロネー三角形分割を表示

はじめに

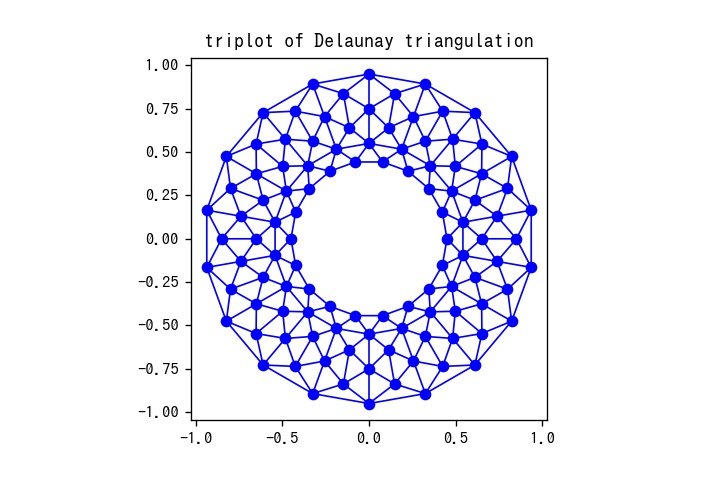
matplotlibのtriplotでデータポイントのドロネー三角形分割を表示する方法について説明する。

コード

	%matplotlib inline
	import matplotlib.pyplot as plt
	import matplotlib.tri as tri
	import numpy as np
	# Create the data.
	n_angles = 18
	n_radii = 6
	min_radius = 0.45
	radii = np.linspace(min_radius, 0.95, n_radii)
	radii
	#array([0.45, 0.55, 0.65, 0.75, 0.85, 0.95])
	angles = np.linspace(0, 2 * np.pi, n_angles, endpoint=False)
	angles
	'''
	array([0. , 0.34906585, 0.6981317 , 1.04719755, 1.3962634 ,
	1.74532925, 2.0943951 , 2.44346095, 2.7925268 , 3.14159265,
	3.4906585 , 3.83972435, 4.1887902 , 4.53785606, 4.88692191,
	5.23598776, 5.58505361, 5.93411946])
	'''
	angles = np.repeat(angles[..., np.newaxis], n_radii, axis=1)
	angles.shape
	#(18, 6)
	angles[:, 1::2] += np.pi / n_angles #swirl data
	x = (radii * np.cos(angles)).flatten()
	y = (radii * np.sin(angles)).flatten()
	# Create the Triangulation; no triangles so Delaunay triangulation created.
	triang = tri.Triangulation(x, y)
	# Mask off unwanted triangles.
	triang.set_mask(np.hypot(x[triang.triangles].mean(axis=1),
	y[triang.triangles].mean(axis=1))
	< min_radius)
	fig1, ax1 = plt.subplots()
	ax1.set_aspect('equal')
	ax1.triplot(triang, 'bo-', lw=1)
	ax1.set_title('triplot of Delaunay triangulation')
	plt.savefig('triplot.jpg',dpi=120)
	plt.show()

view raw Triplot_Demo.py hosted with ❤ by GitHub

解説

モジュールのインポート

	%matplotlib inline
	import matplotlib.pyplot as plt
	import matplotlib.tri as tri
	import numpy as np

view raw Triplot_Demo.py hosted with ❤ by GitHub

データの生成

	# Create the data.
	n_angles = 18
	n_radii = 6
	min_radius = 0.45
	radii = np.linspace(min_radius, 0.95, n_radii)
	radii
	#array([0.45, 0.55, 0.65, 0.75, 0.85, 0.95])
	angles = np.linspace(0, 2 * np.pi, n_angles, endpoint=False)
	angles
	'''
	array([0. , 0.34906585, 0.6981317 , 1.04719755, 1.3962634 ,
	1.74532925, 2.0943951 , 2.44346095, 2.7925268 , 3.14159265,
	3.4906585 , 3.83972435, 4.1887902 , 4.53785606, 4.88692191,
	5.23598776, 5.58505361, 5.93411946])
	'''
	angles = np.repeat(angles[..., np.newaxis], n_radii, axis=1)
	angles.shape
	#(18, 6)
	angles[:, 1::2] += np.pi / n_angles #swirl data
	x = (radii * np.cos(angles)).flatten()
	y = (radii * np.sin(angles)).flatten()

view raw Triplot_Demo.py hosted with ❤ by GitHub

np.repeat(angles[…, np.newaxis], n_radii, axis=1)でanglesをn_radii回、列方向に繰り替えした配列が得られるので、形状は(18, 6)となる。
angles[:, 1::2] += np.pi / n_angles で1列目のデータから一個飛ばしで要素にnp.pi / n_anglesを加える。

ドロネー三角形分割の生成

triang = tri.Triangulation(x, y)

view raw Triplot_Demo.py hosted with ❤ by GitHub

tri.Triangulation(x, y)でドロネー三角形分割が生成される。

ドロネー三角形分割のマスク処理

	triang.set_mask(np.hypot(x[triang.triangles].mean(axis=1),
	y[triang.triangles].mean(axis=1))
	< min_radius)

view raw Triplot_Demo.py hosted with ❤ by GitHub

hypotは２乗和の平方根を返すのでnp.hypot(x[triang.triangles].mean(axis=1), y[triang.triangles].mean(axis=1)) < min_radiusで原点からの距離がmin_radiusより小さいところがTrueとなる。これをmaskするのでTrueの部分で点と線が表示されないこととなる。

triplotでドロネー三角形分割を表示

	fig1, ax1 = plt.subplots()
	ax1.set_aspect('equal')
	ax1.triplot(triang, 'bo-', lw=1)
	ax1.set_title('triplot of Delaunay triangulation')
	plt.savefig('triplot.jpg',dpi=120)
	plt.show()

view raw Triplot_Demo.py hosted with ❤ by GitHub

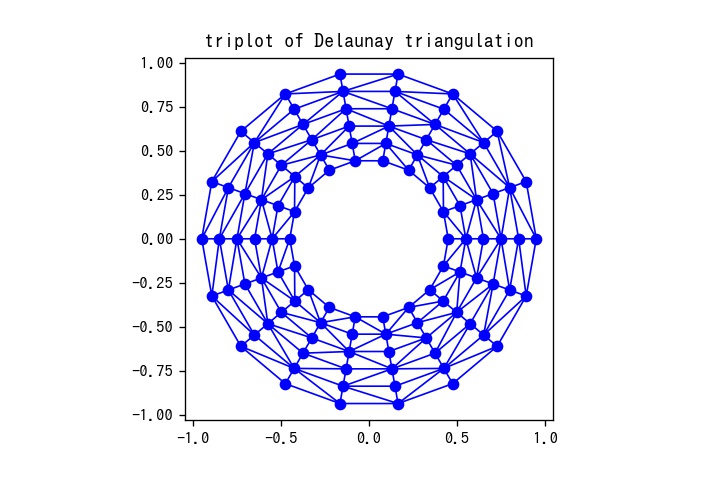
データの一部分を回転させなかったときの図

angles[:, 1::2] += np.pi / n_angles #swirl data
を実行しなかったときの図は下のようになる。

コードをダウンロード(.pyファイル)

コードをダウンロード(.ipynbファイル)

参考

Triplot Demo — Matplotlib 3.1.2 documentation

matplotlib.org

matplotlib.pyplot.triplot — Matplotlib 3.1.2 documentation

matplotlib.org

numpy.hypot — NumPy v2.2 Manual

docs.scipy.org