はじめに
本記事ではクロソイド曲線（Clothoid curve）について解説します。クロソイド曲線は曲率が弧長に比例して増加する特殊な曲線で、道路や鉄道のカーブ設計に広く利用されています。この記事では、クロソイド曲線の数学的な定義を説明し、Pythonのsympyライブラリを使って曲線を計算する方法、そしてmatplotlibのFuncAnimationを使ってアニメーション表示する実装例を紹介します。実用的な応用例も含め、この興味深い曲線についての理解を深めることができるでしょう。
解説
モジュールのインポート
バージョン
Sympyで積分を計算
始点の座標を原点とすると、クロソイド曲線の座標は以下の式で表されます。
\[{\left\{
\begin{array}{}
x(t) = \int_0^t cos (\frac{θ^2}{2})dθ\\
y(t) = \int_0^t sin (\frac{θ^2}{2})dθ
\end{array}
\right.\\
}\]
この式をsympyのintegrateを使用して解くと、以下のような結果が得られます。
座標データの生成
np.arange(-4np.pi, 4np.pi, 0.05)を使って角度を変化させ、各角度における座標を得られた式で計算します。計算した座標はリストに順次追加していきます。
クロソイド曲線の表示
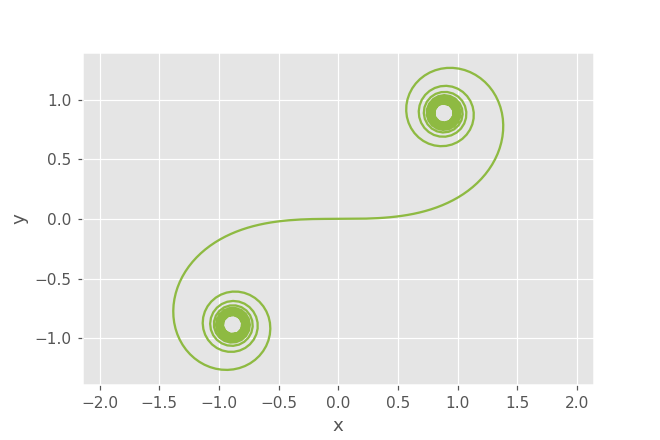
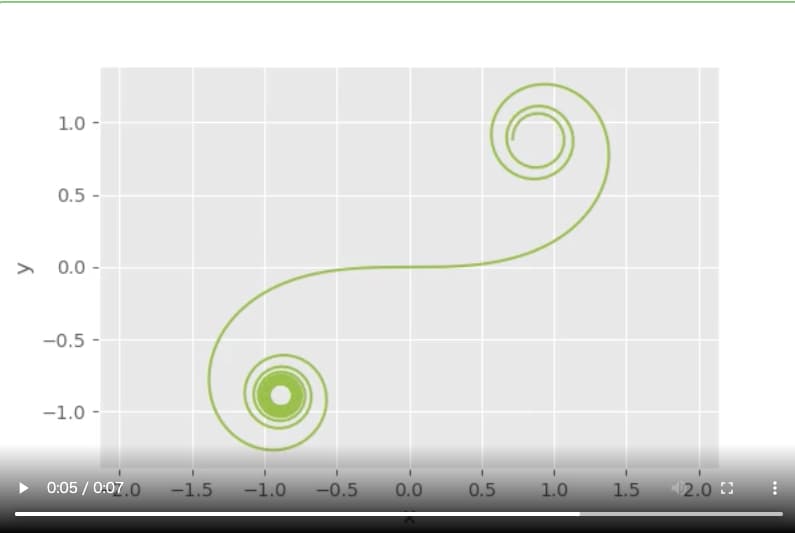
アニメーションで表示
clo, = ax.plot(xx[0], yy[0],”C5-“)でプロットオブジェクトを作成し、clo.set_data()メソッドを使ってデータを更新することでアニメーションを生成します。
まとめ
クロソイド曲線は、数学的に美しいだけでなく実用的な応用も多い曲線です。PythonのsympyとmatplotlibのFuncAnimationを組み合わせることで、この曲線の特性を視覚的に理解することができます。
参考
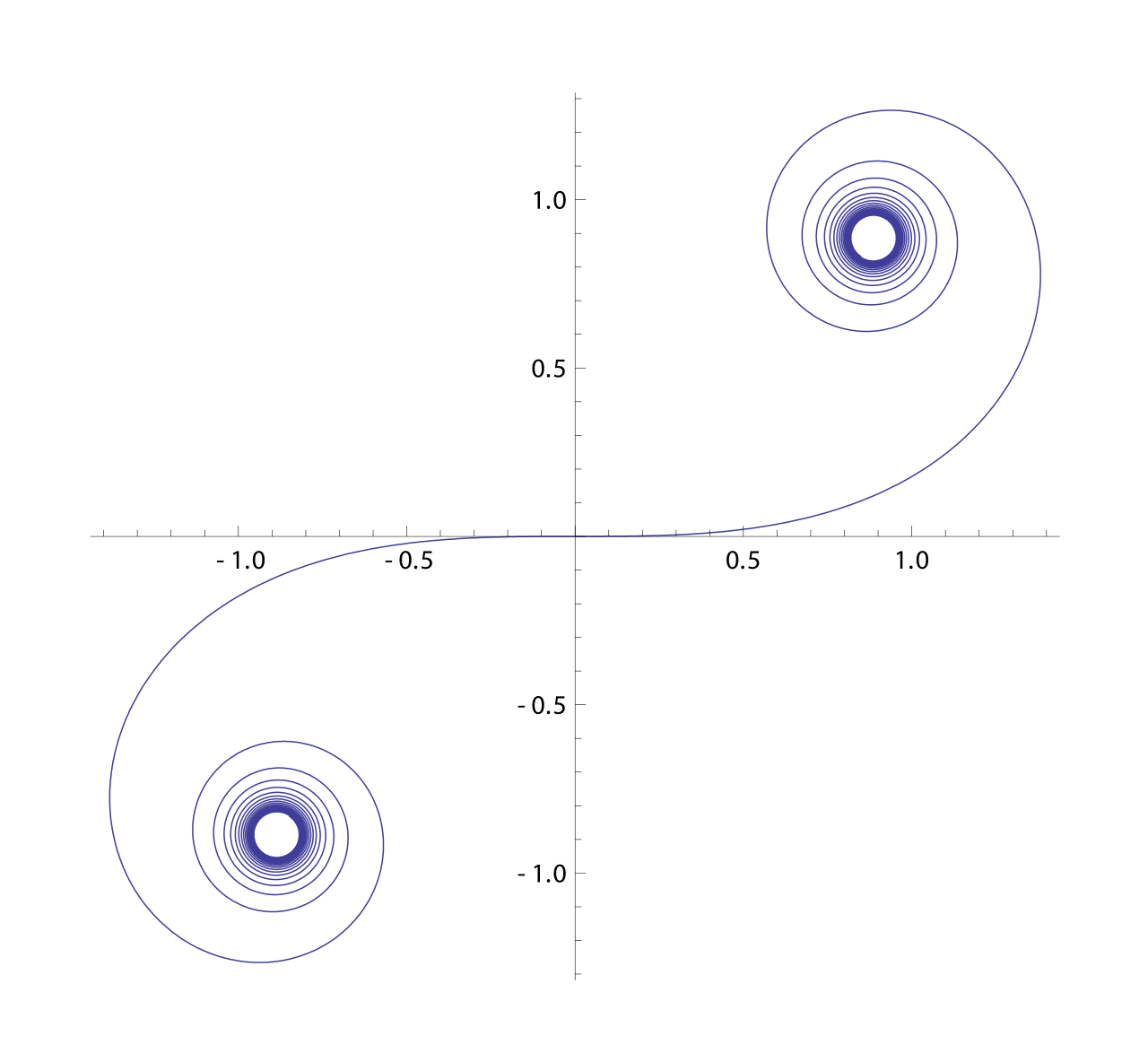
クロソイド曲線 - Wikipedia
ja.wikipedia.org
Integrals - SymPy 1.14.0 documentation
docs.sympy.org
【Python】高速道路のIC/JCTは本当にクロソイド曲線状に建設されているのか？検証してみた - Qiita
はじめに この記事は、趣味で宇宙開発を行う団体「リーマンサット・プロジェクト」の新春アドベントカレンダーです。 私は当団体にて、月面探査などの用途に使用するローバーのソフトウェア開発を担当しています。 リーマンサット・プロジェクトでは、エン...
qiita.com
scipy.special.gamma — SciPy v1.16.1 Manual
docs.scipy.org
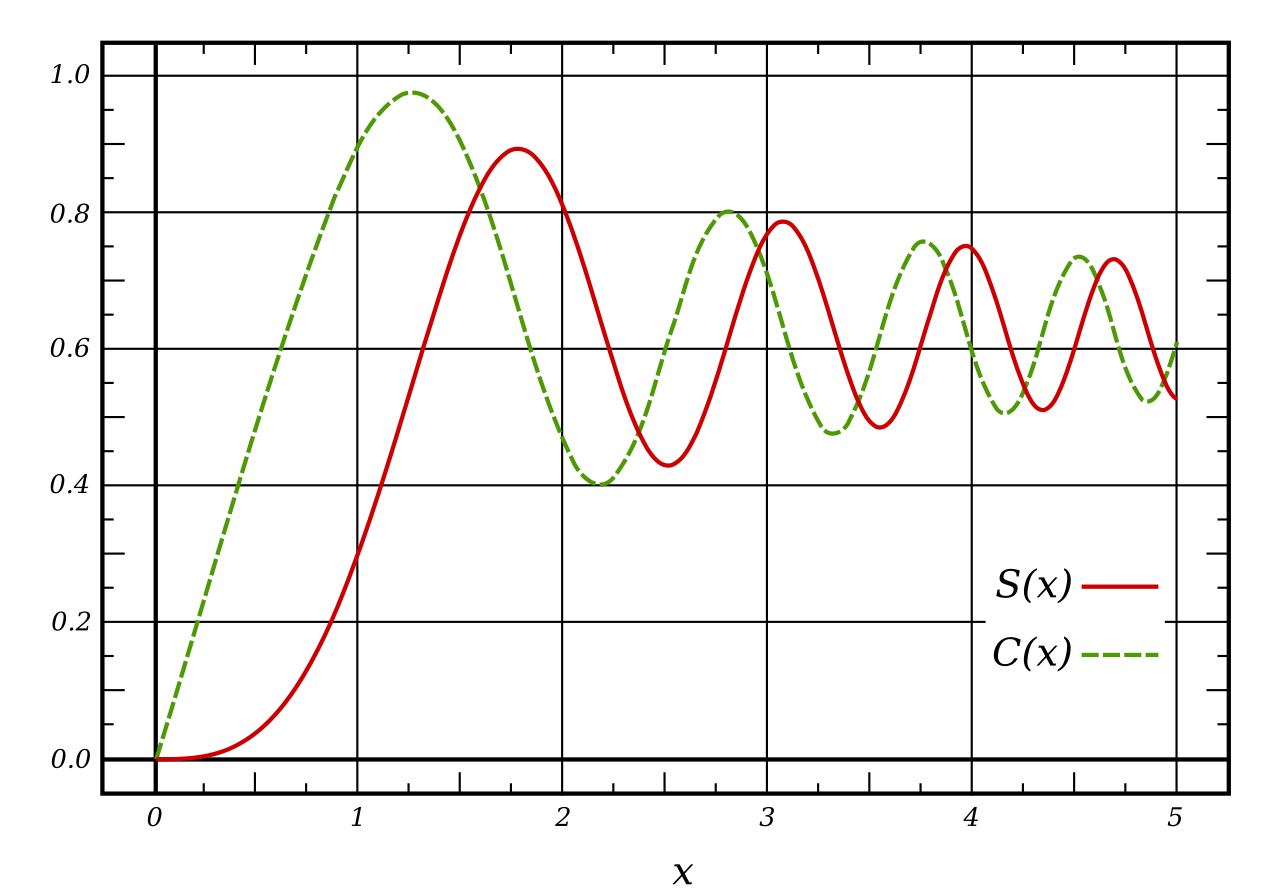
フレネル積分 - Wikipedia
ja.wikipedia.org
コメント