はじめに
matplotlibのmplot3dをつかって、3Dグラフ上にsurface plotで球を表示する方法について解説する。
コード
解説
モジュールのインポート
データの生成
uは0から2πの数列、vは0からπの数列。いずれも100個ある。
x,y,zは球面の方程式を極座標で表した場合で、
となる。
なお直交座標系で半径rの球面は、
で表される。
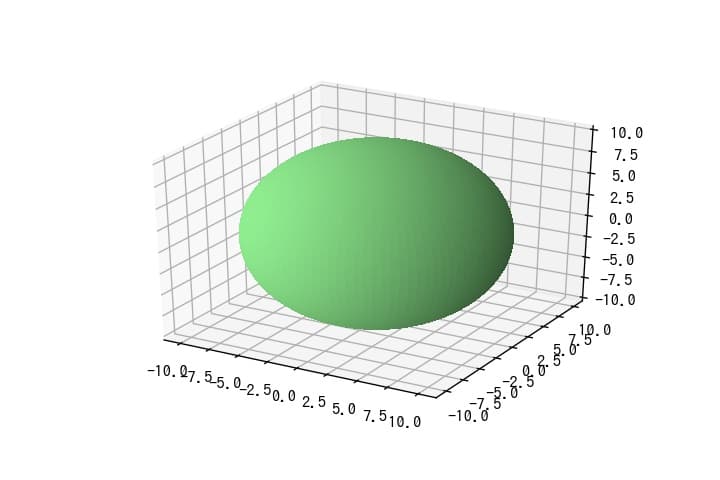
球の表示
アスペクト比を揃えて表示
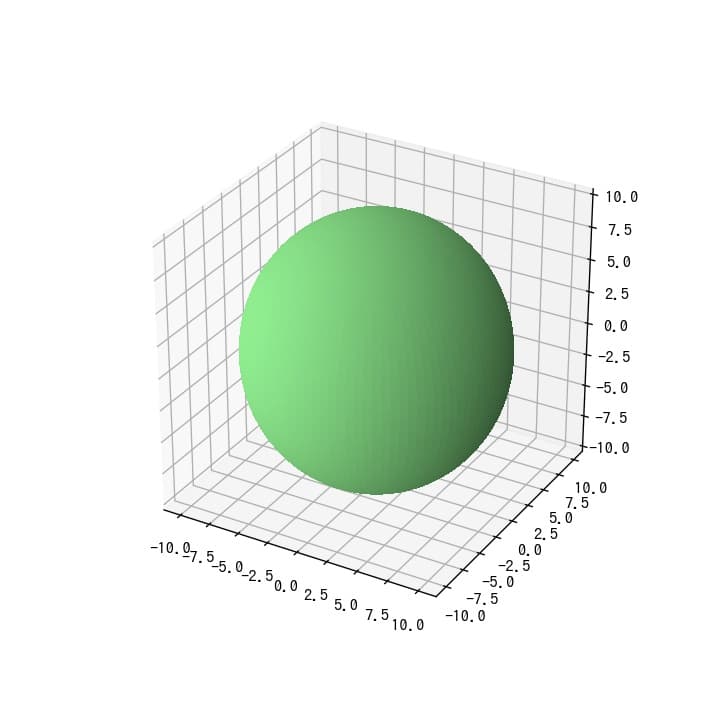
データとしては真球であるのに対して、見た目が楕円球となっているので図のアスペクト比を揃えることを試みた。最初に下記のコードを実行すると、
ax.set_aspect('equal')
でエラー(NotImplementedError)となり、うまく行かない。そこでfigsizeでアスペクト比を揃えてグラフを表示することで真球を表示することができた。
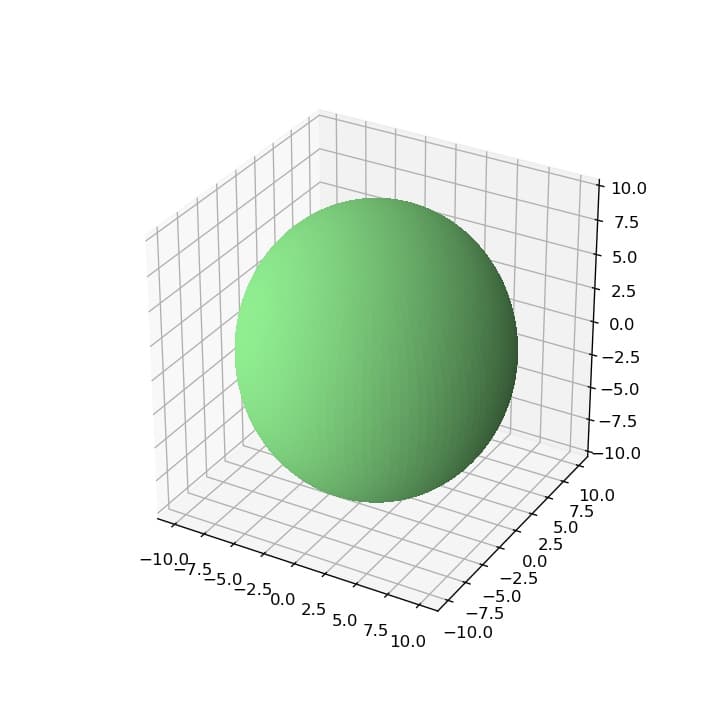
set_box_aspectを利用する
matplotlib3.3以降では、set_box_aspectにより3Dグラフのアスペクト比を変えることができる。
参考
3D surface (solid color) — Matplotlib 3.10.3 documentation

球面の方程式に関する5つの公式と具体例 | 高校数学の美しい物語
球面の方程式に関する公式総まとめ。空間座標での表現,標準形,ベクトル方程式,直径の両端が分かっている場合など。
matplotlib.axes.Axes.set_box_aspect — Matplotlib 3.10.3 documentation

コメント
[…] [matplotlib 3D] 18. 3D surfaceプロットで球を表示matplotlibのmplot3dをつかって、3Dグラフ上にsurface plotで球を表示する方法について解説する。sabopy.com2018.10.17 […]
[…] [matplotlib 3D] 18. 3D surfaceプロットで球を表示matplotlibのmplot3dをつかって、3Dグラフ上にsurface plotで球を表示する方法について解説する。sabopy.com2018.10.17 […]