はじめに
構造化されてない3次元データの等高線を表示するtricontourについて解説する。
コード
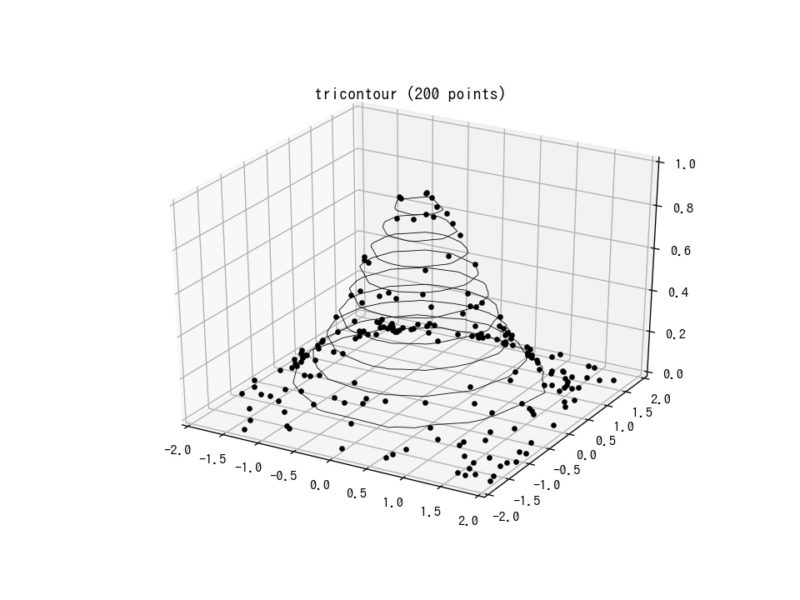
解説
モジュールのインポート
バージョン
データの生成
np.random.uniform(-2, 2, npts)により-2以上,2未満のデータをnpts(200)個生成する。
3D Tricontourグラフの作成
ax.tricontour(x, y, z)で整っていないデータを近似して、等高線を表示できる。
ax.plot(x, y, z, ‘ko’, ms=3)でデータを黒丸で示している。
回転アニメーション
tricontourではなくcontourで非構造データの等高線を表示
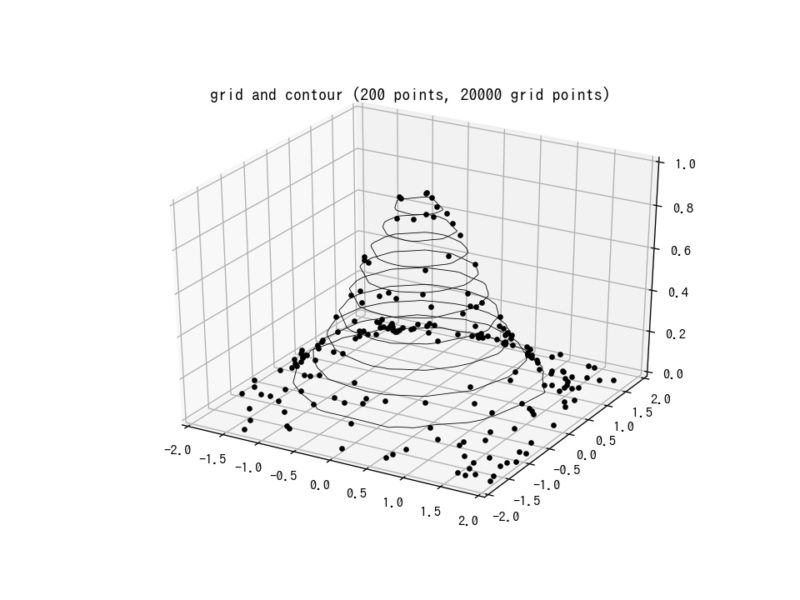
等間隔なgridを作成して、それでzデータポイントを補間することで構造化されたデータを作成している。補間にはLinearTriInterpolatorを用いた。LinearTriInterpolatorは三角形グリッドで線形補間する方法となっている。tricontourと同じグラフが得られている。
コードをダウンロード(.pyファイル) コードをダウンロード(.ipynbファイル)参考
matplotlib.axes.Axes.tricontour — Matplotlib 3.1.2 documentation
Contour plot of irregularly spaced data — Matplotlib 3.1.2 documentation
matplotlib.tri — Matplotlib 3.1.2 documentation

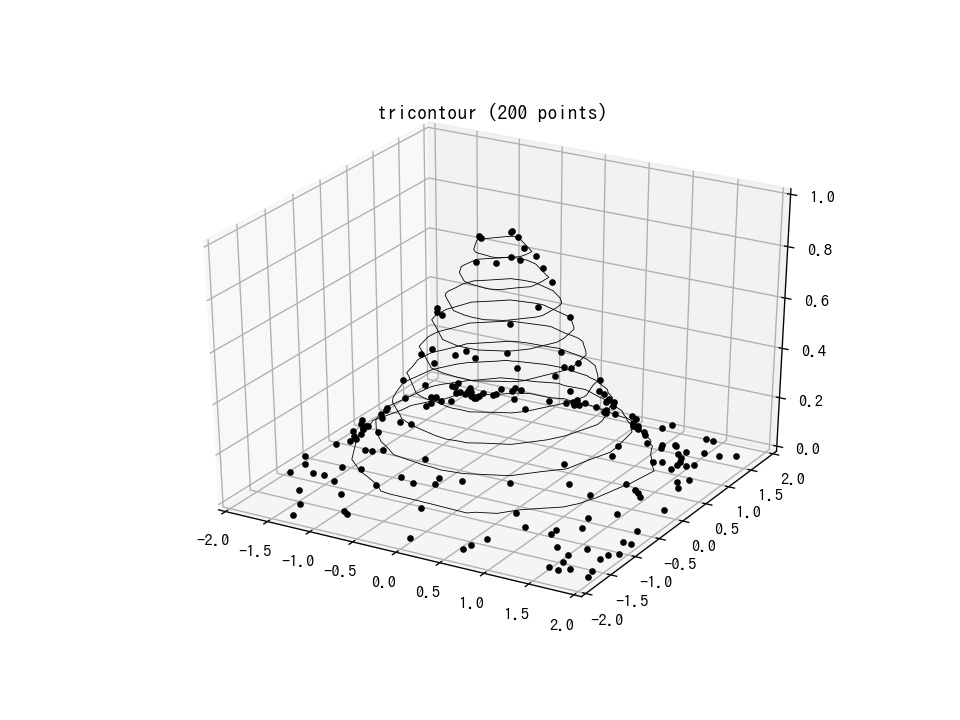
コメント
[…] [matplotlib 3D] 22. 3D tricontourを塗りつぶしにした図。 […]