[matplotlib 3D] 31. トーラス（ドーナツ形状）を3Dボクセル表現する方法

はじめに

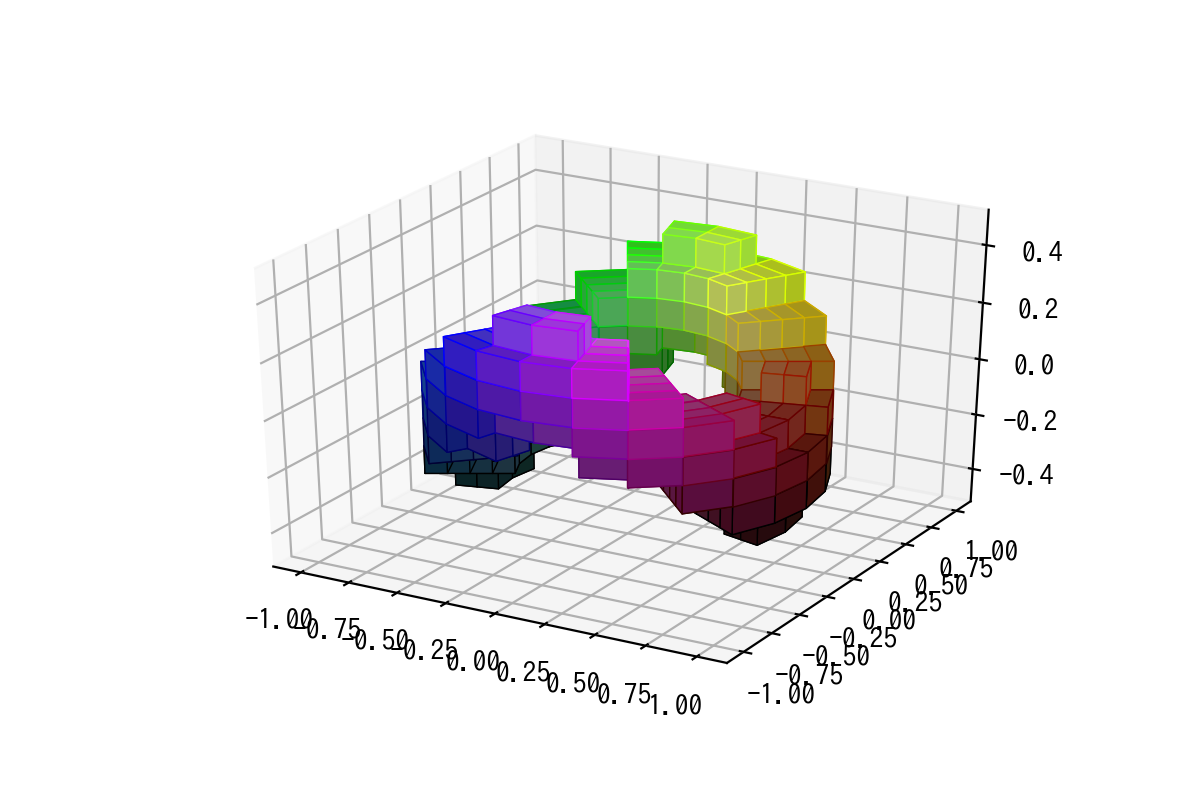
トーラス（英: Torus）は、3次元空間における円環体のことで、数学的には円を別の円の周りに回転させて得られる曲面です。このチュートリアルでは、matplotlibのvoxels関数を使用して、この美しい幾何学的形状をボクセル（3次元ピクセル）で表現する方法を解説します。

コード

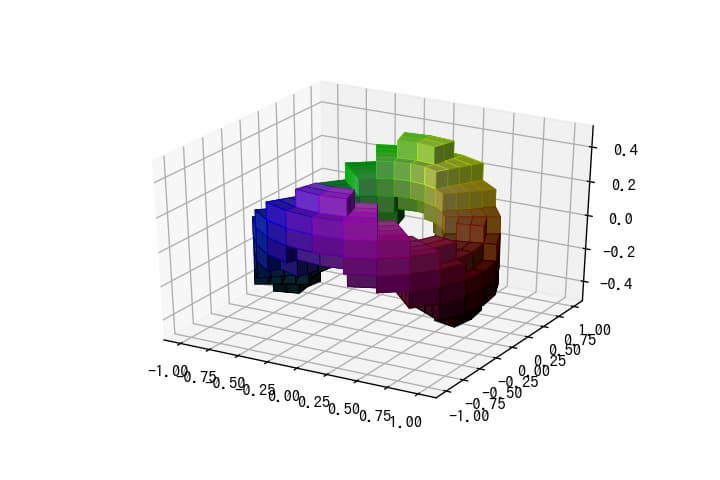
解説

データの生成

トーラスとはドーナツの形状のことであり、直交座標系では以下の数式で表現できる。Rは中心から外周までの主半径、rはドーナツの断面の副半径となる。

$$(\sqrt{x^2 + y^2} – R)^2 + z^2 = r^2$$

関数midpoints(x)は、[matplotlib 3D] 30. voxels_rgbで既に定義したものと同一です。

[matplotlib 3D] 30. voxelグラフでRGB色空間を可視化

Matplotlibの3Dグラフ機能を使って、RGB色空間をvoxelグラフで可視化する方法を解説します。3次元空間での色の分布を理解し、視覚的に表現することで、色彩理論への理解を深めることができます。

sabopy.com

r, theta, z = np.mgrid[0:1:11j, 0:np.pi*2:25j, -0.5:0.5:11j]

jは複素数のjとなっています。

x = r*np.cos(theta)
y = r*np.sin(theta)

x,yは円筒座標からの変換を行っています。

sphere = (rc - 0.7)**2 + (zc + 0.2*np.cos(thetac*2))**2 < 0.2**2

ここで、0.2np.cos(thetac2)は「揺れる」トーラス（ぐらぐらしたドーナツ形状）を生成するために追加しています。<0.2**2と比較することで、トーラスの部分だけをTrueに設定している。

色の設定

hsv = np.zeros(sphere.shape + (3,))

HSVの色の設定も[matplotlib 3D] 30. voxels_rgbと同じになっています。

colors = matplotlib.colors.hsv_to_rgb(hsv)

HSVからRGBへ変換することができます。変換元のHSV値は0〜1の範囲で指定する必要があります。[2]

トーラスの表示

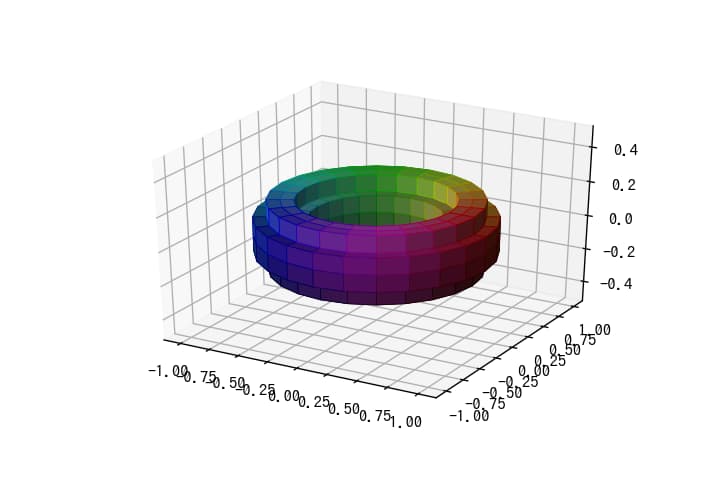
歪んでないトーラス

sphere = (rc - 0.7)**2 + zc**2 < 0.2**2

このようにすることで、歪みのないトーラスを生成できます。

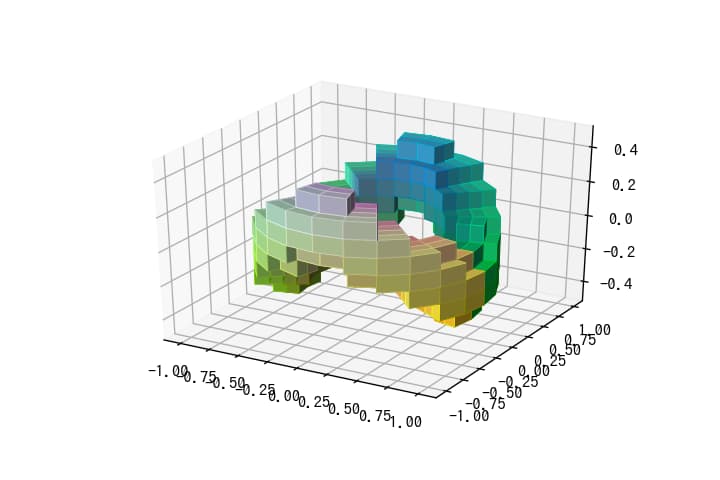
hsvのままプロット(colors = hsv)

コードをダウンロード(.pyファイル)

コードをダウンロード(.ipynbファイル)

参考

トーラス - Wikipedia

ja.wikipedia.org

3D voxel / volumetric plot with cylindrical coordinates — Matplotlib 3.1.0 documentation

matplotlib.org

Python, complex型で複素数を扱う（絶対値、偏角、極座標変換など） | note.nkmk.me

Pythonには複素数を扱うためのcomplex型が標準で用意されている。 単純な計算だけならモジュールをインポートする必要はないが、標準ライブラリcmathをインポートすると複素数に対応した数学関数（指数・対数・三角 ...

note.nkmk.me

matplotlib.colors.hsv_to_rgb — Matplotlib 3.10.5 documentation

matplotlib.org