はじめに
NumPyを使用して、ランダムに配置された点の集合から各点の最近傍点を見つけ出し、それらを線で結ぶ方法について解説します。
コード

解説
データの生成
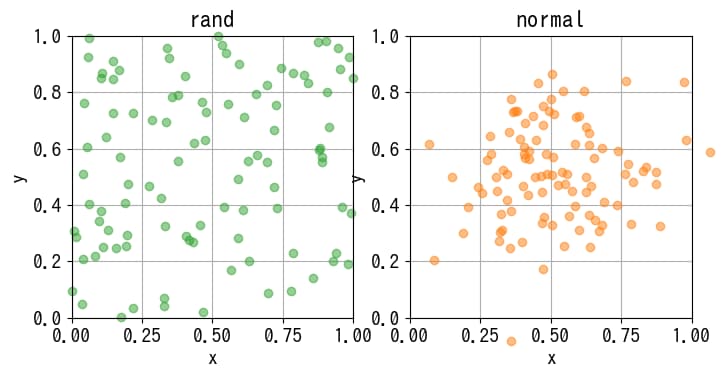
一様分布に従う乱数x2と、平均0.5・標準偏差0.2の正規分布に従う乱数x3を生成しました。どちらもサイズは(100,2)に設定しています。
生成した配列の可視化
2乗距離の計算
ブロードキャストと集約関数を組み合わせて効率的に2乗距離を計算します。
x2[:, np.newaxis, :] と x2[np.newaxis, :, :]はそれぞれ形状(100, 1, 2)と(1, 100, 2)になります。これらをブロードキャストで演算することで、すべての点の組み合わせにおける座標ごとの差を一度に計算できます。
この差を**2で2乗し、合計することで2乗距離が得られます。
np.sum()でaxis=-1を指定すると、3次元配列(形状=(100, 100, 2))の最後の次元([:, :, 0]と[:, :, 1])を合計できます。
近傍点の座標
np.argsort()を2乗距離の配列に適用することで各点に最も近い座標のインデックスを取得できます。
最近傍の点の可視化

上記コードで各点における最も近い点との間に線をプロットできます。
コードをダウンロード(.pyファイル) コードをダウンロード(.ipynbファイル)
コメント