はじめに
画像処理において、フーリエ変換は空間領域から周波数領域への変換として重要な役割を果たします。しかし、画像の境界で不連続性が生じると、周波数スペクトルに望ましくないアーティファクトが発生することがあります。
この問題を解決するために、scikit-imageのskimage.filters.window関数を使用して窓関数(ウィンドウ関数)を適用することができます。窓関数は画像の境界付近の値を徐々に0に近づけることで、不連続性を滑らかにします。
ここでは、skimage.filters の windowを画像のフーリエ変換に適用する方法について説明します。
窓関数の種類
skimage.filters.windowでは、以下のような様々な窓関数が利用可能です:
- ガウス窓(Gaussian)
- ハニング窓(Hanning)
- ハミング窓(Hamming)
- バートレット窓(Bartlett)
- ブラックマン窓(Blackman)
解説
モジュールのインポートなど
バージョン
画像の読み込み
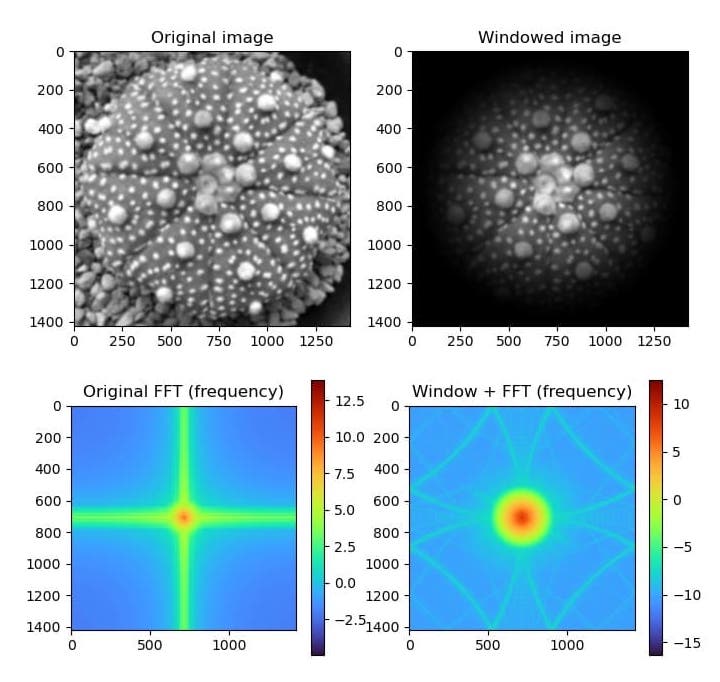
この例では、アストロフィツム属の兜丸の写真を使用し、rgb2gray関数でグレースケール画像に変換します。

窓関数をかける
まず、Gaussianフィルターを使用してノイズを滑らかにし、その後に窓関数を適用します。ここでは、SciPyの窓関数の一つである’hann’を使用しています。その他の利用可能な窓関数については、下記のページで確認できます。
フーリエ変換
scipyのfft2でフーリエ変換をします。
結果の表示
左上が元画像、右上が窓関数を適用した画像です。左下は元画像のフーリエ変換結果、右下は窓関数を適用した画像のフーリエ変換結果を示しています。窓関数の効果により、十字模様のアーティファクトが消え、より鮮明な結果が得られています。
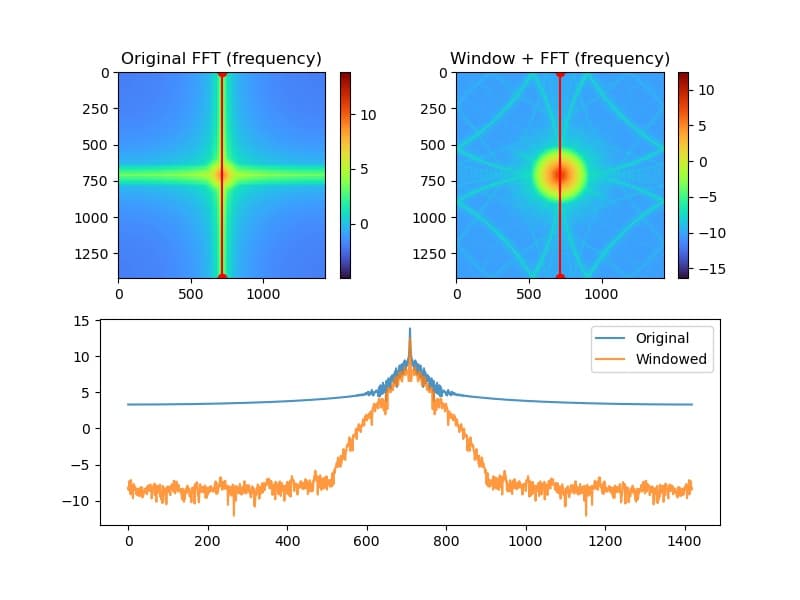
縦に線分析
縦方向のラインプロファイルは以下のようになります。
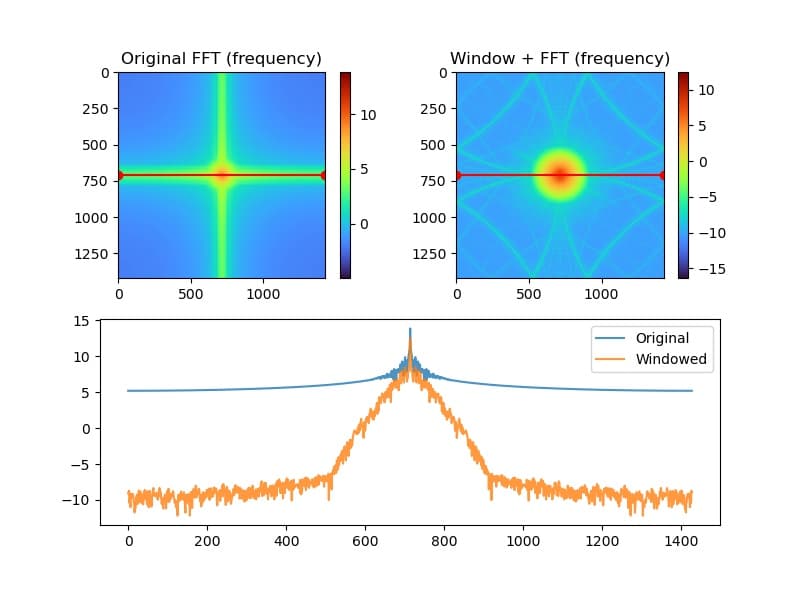
横に線分析
横方向のラインプロファイルは以下のようになります。
まとめ
窓関数の効果
窓関数を適用することで以下のような効果が得られます:
- 周波数スペクトルにおけるクロストーク(漏れ)の低減
- スペクトル漏れによる偽のピークの抑制
- 周波数分解能の向上
実践的な応用例
窓関数の適用は、以下のような画像処理タスクで特に有効です:
- 画像のノイズ除去
- 特定の周波数成分の強調または抑制
- パターン認識やテクスチャ分析
- 画像の圧縮や復元
注意点
窓関数を使用する際には、以下の点に注意が必要です:
- 窓関数の適用により、画像の境界付近の情報が失われる可能性がある
- 適切な窓関数の選択は、処理対象の画像や目的によって異なる
- 窓関数のパラメータ調整が必要な場合がある
scikit-imageの窓関数を活用することで、フーリエ変換を用いた画像処理の精度と安定性を向上させることができます。

コメント