はじめに
scipyのintegrate.solve_ivp関数は、常微分方程式の初期値問題を数値的に解くための強力なツールです。この関数は、様々な数値解法に対応しており、高精度な結果を得ることができます。
コード
解説
モジュールのインポート
バージョン
定数を定義
mは質量、kは抗力係数、gは重力加速度としました。
初期値の設定
初期値を設定します。状態変数(x,y,vx,vy)として、位置(0,0)から速度(20,20)で物体を打ち上げることにしました。
関数の定義
微分方程式を定義します。空気抵抗による力は F = -kv で表されるため、ニュートンの運動方程式から以下の式が導出できます。
\[m \cdot u” = F + mg\]
式を変換すると、以下のようになる。
\[u” = -\frac{k}{m} u’ + g\]
x成分は右辺の第1項のみですが、y成分は重力加速度が加わるため第1項と第2項の合計となります。
solve_ivpで解く
t_spanは時間の(開始、終了)を表し、tは実際に計算に使用する時間配列を指定します。t_evalパラメータにtを設定できますが、省略した場合は自動的に適切な間隔で計算が行われます。その他の変数(ここではk)はargs=(k,)の形式で渡します。v0は初期値を表します。
solve_ivp(f, t_span, v0, t_eval=t, args=(k,))を呼び出すことで微分方程式を解きます。
結果は以下のようになります。
結果の表示
ind = solved_data.y[1]>=0 を使用して、y が正の値のみを抽出して表示しています。 解析結果は solved_data.y[0][ind] のような形式でアクセスできます。
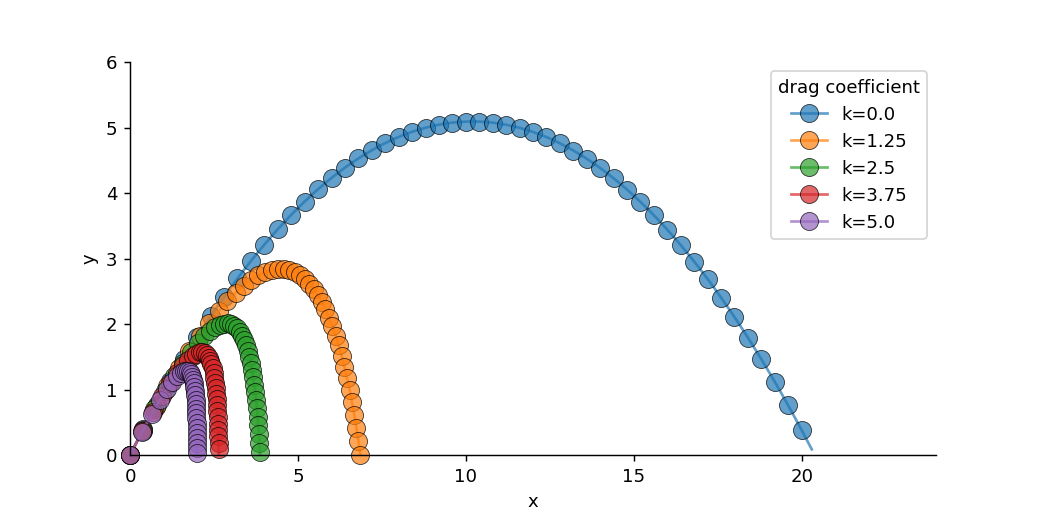
抗力係数 k=1 の場合、x と y の関係は下図のようになります。空気抵抗により、x 方向の移動距離が抑制されていることがわかります。

kを変えた時の変化
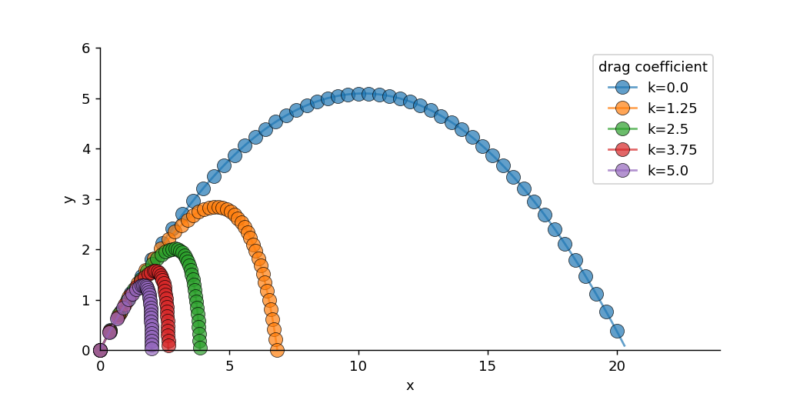
k の値を np.linspace(0., 5., 5) で変化させて計算した結果は以下のようになります。

このときのx方向の速度の経時変化は以下のようになります。時間はsolved_data.tから取得できます。抵抗が大きい場合、速度が徐々に0に収束していく様子が明確に観察できます。
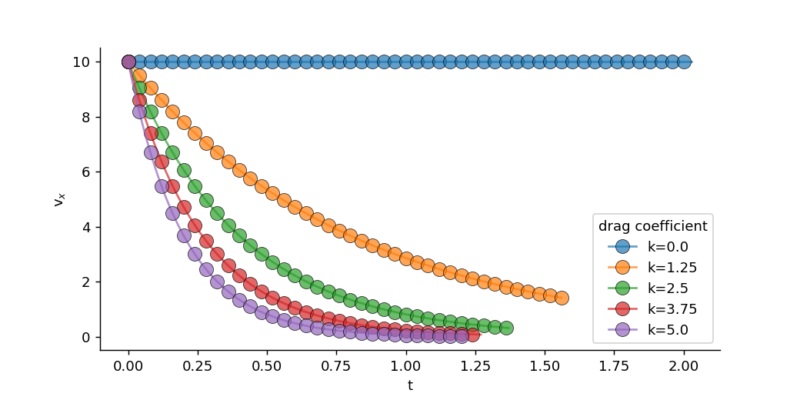
このときのy方向の速度の経時変化は以下のようになります。

k=5の場合の結果から、終端速度が一定値に収束していることが明確に観察できます。
コードをダウンロード(.pyファイル) コードをダウンロード(.ipynbファイル)
コメント