はじめに
本記事では、lmfitライブラリを使用して減衰発振器モデルによるカーブフィッティングを行う方法について解説します。非線形最小二乗法の応用として、振動減衰する信号データに対する数学モデルの適用方法と、パラメータ推定の実践的なアプローチを紹介します。
コード
解説
モジュールのインポート
バージョン
データの生成
\[ f(x; A, \mu, \sigma) = \frac{A}{\sqrt{ [1 – (x/\mu)^2]^2 + (2\sigma x/\mu)^2}}\]
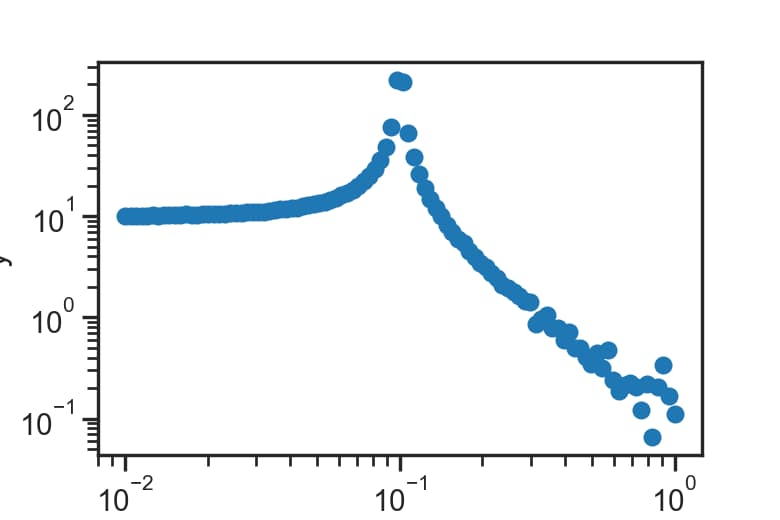
前述の関数を使用してデータを生成します。生成されたデータは以下のようになります。
モデルの定義
lmfit.models モジュールの
DampedOscillatorModel をモデル関数として使用します。
初期パタメータの推定
model.guess(y, x=x)により、初期値を推定します。
カーブフィット
out = damp_mod.fit(y, pars, x=x)を実行して、カーブフィッティングを行います。
フィッティング結果の表示
print(result.fit_report())を使用して、フィッティングの結果を確認できます。
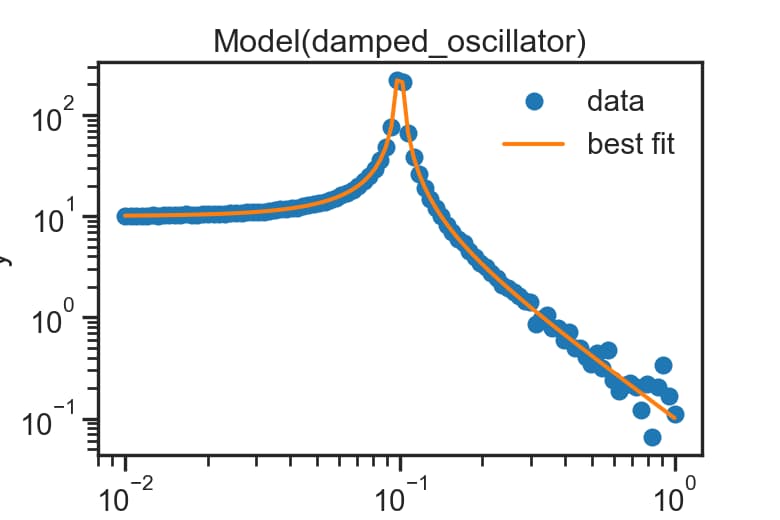
result.plot_fit()を実行することで、データポイントとフィッティングカーブが視覚的に表示されます。

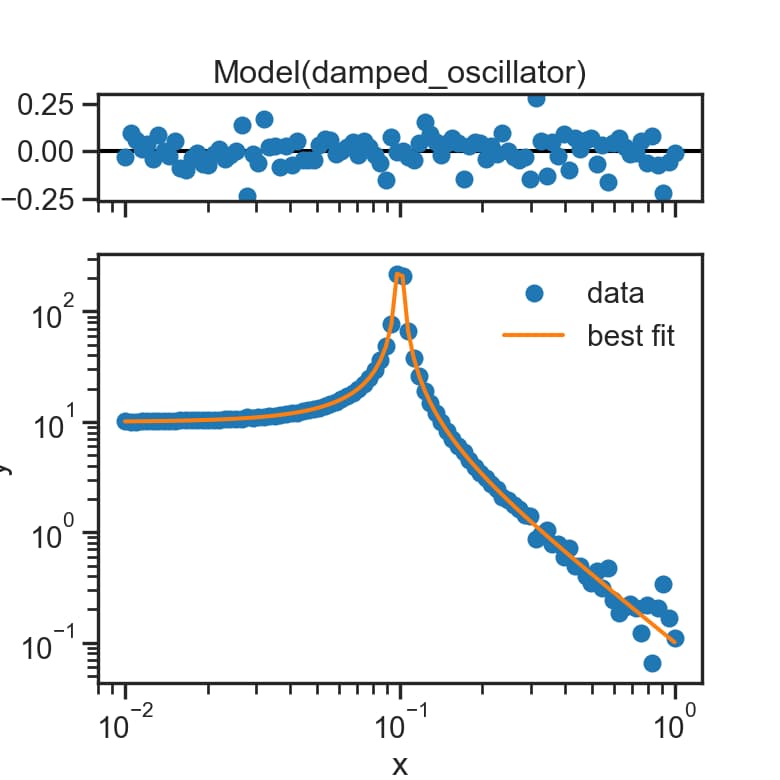
result.plot()を実行すると、フィッティング結果とともに残差が表示されます。
まとめ
lmfitライブラリを用いた減衰発振器モデルによるカーブフィッティングについて解説しました。このアプローチにより、振動減衰する現象を数学的に記述し、実験データから物理パラメータを高精度に抽出することが可能になります。科学研究や工学分野での信号解析に役立つ手法として活用できるでしょう。
参考
Built-in Fitting Models in the models module — Non-Linear Least-Squares Minimization and Curve-Fitting for Python

コメント