[lmfit] 9. 対数正規分布関数に基づくモデルによるカーブフィッティング

はじめに
コード
解説
まとめ
参考

はじめに

lmfitは非線形最小二乗法を用いてカーブフィットするためのPythonライブラリであり、Scipy.optimize.curve_fitの拡張版として位置づけられています。本記事では、lmfitを使用して対数正規分布関数に基づくモデルによるカーブフィッティングの方法を詳しく解説します。

コード

解説

モジュールのインポートなど

バージョン

対数正規分布データの生成

まず、default_rng()関数でランダム生成器（rng）を初期化し、rng.lognormalメソッドを使って対数正規分布に従うデータを生成します。その後、np.histogramでデータをヒストグラム化して対数正規分布を得ます。以下の図はその結果を示しています。

モデルの定義

lmfit.models の LognormalModelをモデル関数として用います。

初期パタメータの推定

model.guess(histo, x=bins)を使用して、上図の対数正規分布のフィッティングパラメータの初期値を推定します。この結果得られるパラメータ(params)は以下の通りです。

カーブフィット

model.fit(histo, params, x=bins)により、カーブフィッティングを実行します。

フィッティング結果の表示

print(result.fit_report())により、フィッティングの結果を確認することができます。

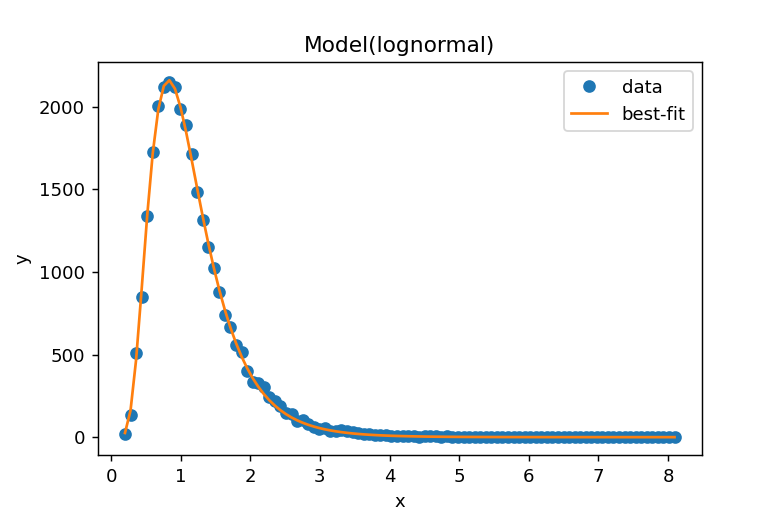
result.plot_fit()によりデータとフィッティングカーブが表示されます。

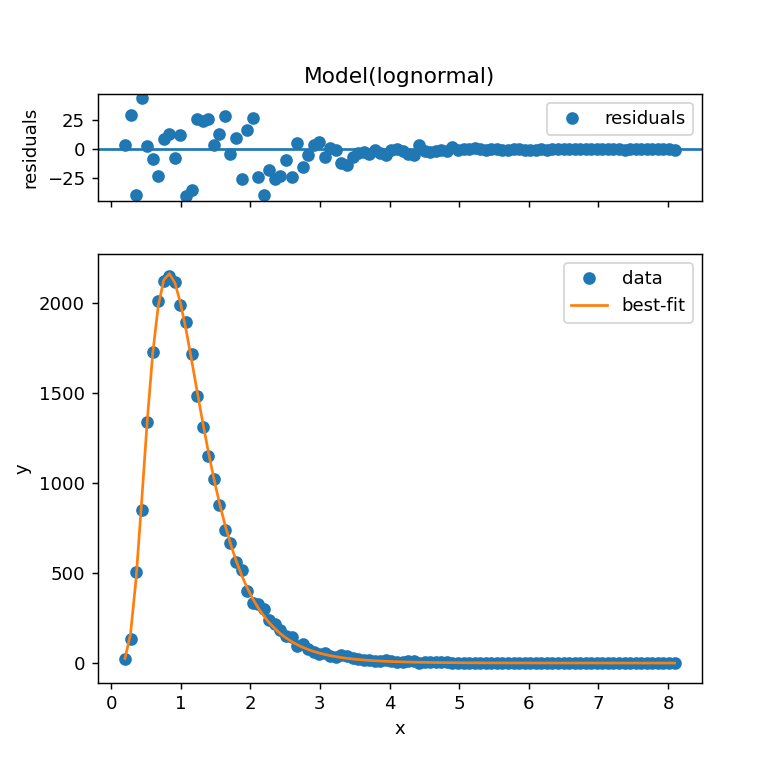
result.plot()とすることで残差とともにフィッティング結果が表示されます。

コードをダウンロード(.pyファイル)

コードをダウンロード(.ipynbファイル)

まとめ

本記事では、lmfitライブラリを用いた対数正規分布関数によるカーブフィッティングの方法について解説しました。対数正規分布モデルの構築、パラメータの初期設定、最適化プロセス、そして結果の評価と解釈までの一連の流れを示しました。このアプローチは、非対称な分布を持つデータの分析に特に有効であり、科学研究やデータ分析の様々な場面で応用できます。