はじめに
トーラス結び目は、ドーナツ形状（トーラス）の表面上に描かれる特殊な曲線です。この結び目は2つの整数パラメータ p と q で特徴付けられ、(p,q)-トーラス結び目と表記されます。pとqが互いに素である場合、曲線は1周して元の位置に戻ります。ここでは、matplotlib 3Dモジュールを使用してトーラス結び目（トーラスノット）を視覚化する方法を解説します。
コード
解説
トーラス結び目について
https://amzn.to/2UlYkRJ
amzn.to
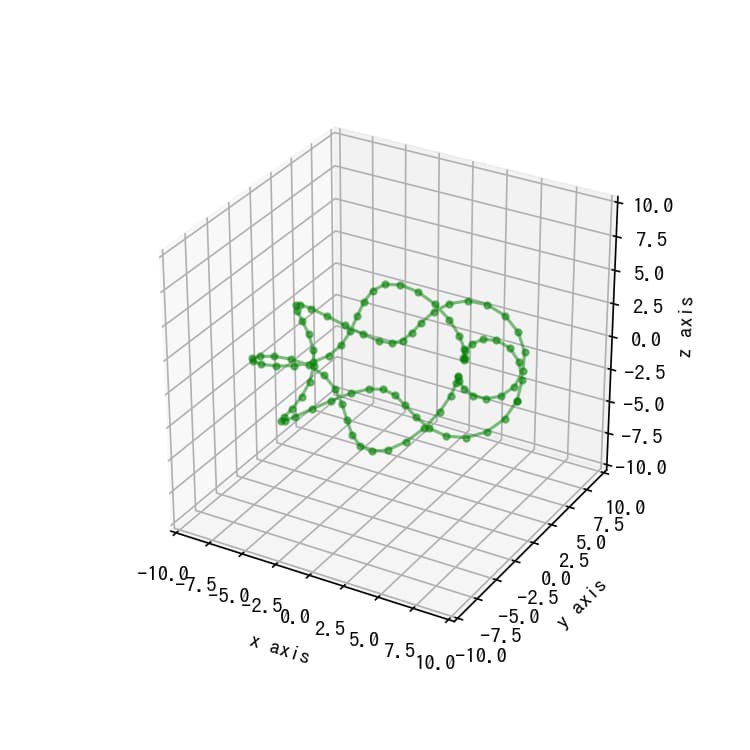
上記の参考図書に記載されているパラメトリック方程式を用いて、トーラス結び目を視覚化しました。
トーラス結び目は以下の数式で表現できます。
$$x = (b+asin(pu))cos(qu)\\ y = (b+asin(pu))sin(qu)\\ z = asin(pu)$$トーラス結び目はパラメトリック方程式でデータを生成します。媒介変数uは、np.linspace(0,2*np.pi,100)として0から2πの範囲で設定します。この式において、bはトーラス自体の大きい半径、aはトーラスの太さの半径を表します。
この式によって描画されるのは曲面ではなく、トーラス曲面に沿った曲線です。
パラメータpとqは、それぞれ小円方向にp回、大円方向にq回巻くことを表す定数です。
モジュールのインポート
figの作成
トーラス結び目の生成,表示
可視化には、plot(X,Y,Z)関数を使用して散布図で表現しています。’g.-‘というスタイル指定により、トーラス結び目が緑色の点と線で表示されます。
軸範囲、軸ラベル、アスペクト比の設定
回転アニメーション
作製した図を回転させると以下のようになります。
回転アニメーションは以下の記事を参考にして作成しました。
[matplotlib 3D] 14. 3Dグラフの回転アニメーション
matplotlibのmplot3dを使用して3Dグラフの回転アニメーションを作成する方法を解説します。動画として保存する手順や回転角度の制御など、3Dビジュアライゼーションを動的に表現するための基本テクニックを紹介します。
sabopy.com
2018.10.25
まとめ
トーラス結び目は数学的な美しさと複雑さを兼ね備えた対象であり、matplotlibの3Dプロット機能を使うことで簡単に視覚化できます。パラメータを変更することで様々な形状を試すことができるため、数学的な探求や芸術的な表現に活用できます。
コメント