[matplotlib] 52. 対数正規分布データのヒストグラムに最頻値、中央値、平均値を表示

はじめに
コード
解説
まとめ
参考

はじめに

この記事では、NumPyを使用して対数正規分布に従うデータを生成し、Matplotlibを用いてそのヒストグラムを作成します。さらに、データの最頻値、中央値、平均値を計算し、これらの統計値をヒストグラム上に視覚的に表示する方法を詳しく解説します。対数正規分布の特性を理解し、実際のデータ分析に応用するための基本を学びましょう。

コード

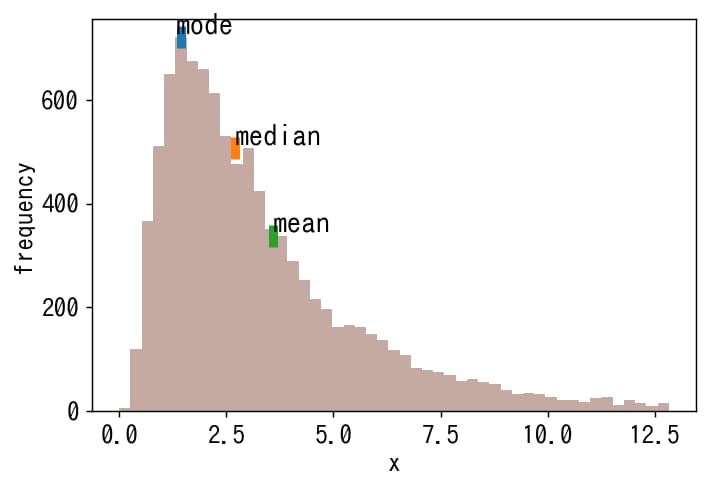
解説

モジュールのインポート

データの生成

np.random.lognormal(mu, sigma, 10000)関数を使用して対数正規分布に従うランダムな要素を生成します。ここで、muは対数のパラメータの平均、sigmaは標準偏差を表します。生成したデータの主な統計値は以下のようになります。これらの統計量はdescribe()メソッドで簡単に取得できます。

	count	mean	std	min	25%	50%	75%	max
0	10000.0	3.596309	3.209368	0.18162	1.619376	2.66991	4.44486	48.417122

DataFrameから平均と中央値を.ilocを使用してスライスで取得できます。これによりnp.arrayと同様の方法でデータにアクセスできます。

ヒストグラムの表示

ヒストグラムのビンはbins = np.linspace(0, np.percentile(data, 98))と設定することで、0からデータの98パーセンタイルまでの範囲を指定しています。ヒストグラムはfreq, binn, _ = ax.hist(data, bins=bins, color='C5', alpha=0.5, clip_on=False)で描画でき、freqが頻度値となります。最頻値はヒストグラムのピーク値に該当するため、np.argmax(freq)を使って頻度が最大となるインデックスを取得し、ヒストグラムデータを基にグラフ上に垂直線をプロットします。

同様に、中央値と平均値も垂直線でプロットします。np.where(bins>median)[0][0]を使用することで、中央値より大きい最初のビンのインデックスを取得できます。

コードをダウンロード(.pyファイル)

コードをダウンロード(.ipynbファイル)

まとめ

本記事では、NumPyとMatplotlibを使って対数正規分布データを生成し、そのヒストグラムに最頻値、中央値、平均値を視覚的に表示する方法を解説しました。これらの統計値を視覚化することで、データの分布特性をより直感的に理解できます。データ分析や統計学の学習に役立つテクニックとして活用してください。