はじめに
scipy.integrateのtrapezoid、 simpson、cumulative_trapezoid、rombで離散的データの数値積分をする方法について説明する。
コード
解説
モジュールのインポート
バージョン
データの生成
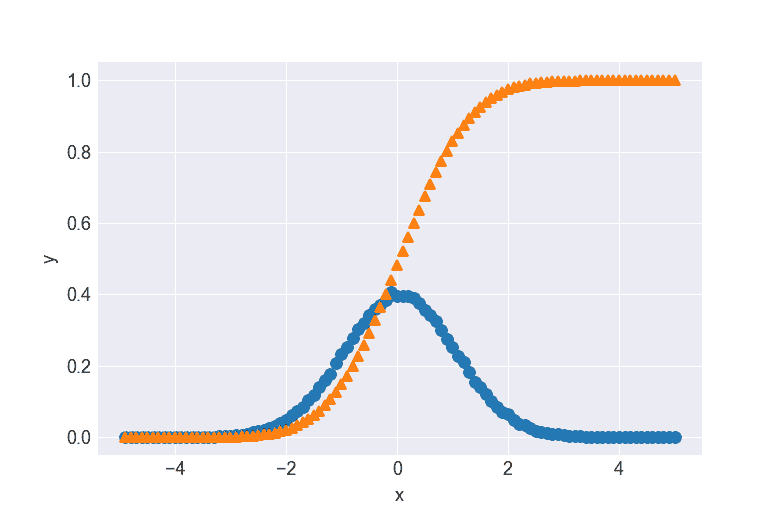
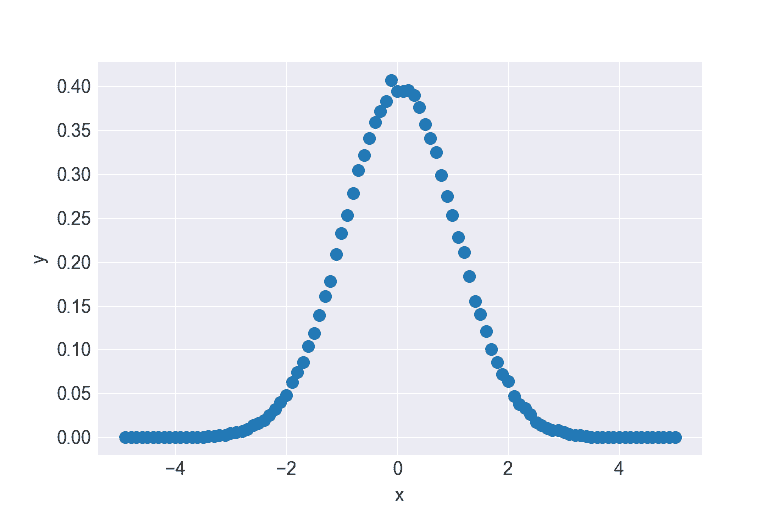
データを図で表示
trapezoidによる積分
台形公式により積分を行なった結果が得られる。
simpsonによる積分
シンプソンの公式を使った積分値が得られる。
cumulative_trapezoidによる積分
cumulative_trapezoidにより、各区間の累積積分値を求めることができる。図示すると上のようになる。
rombによる積分
rombでロンバーグ積分を計算できる。データ数が2**k + 1である必要がある。
コードをダウンロード(.pyファイル) コードをダウンロード(.ipynbファイル)参考
romb — SciPy v1.14.1 Manual
docs.scipy.org
cumulative_trapezoid — SciPy v1.14.1 Manual
docs.scipy.org
simpson — SciPy v1.14.1 Manual
docs.scipy.org
trapezoid — SciPy v1.14.1 Manual
docs.scipy.org
コメント