はじめに
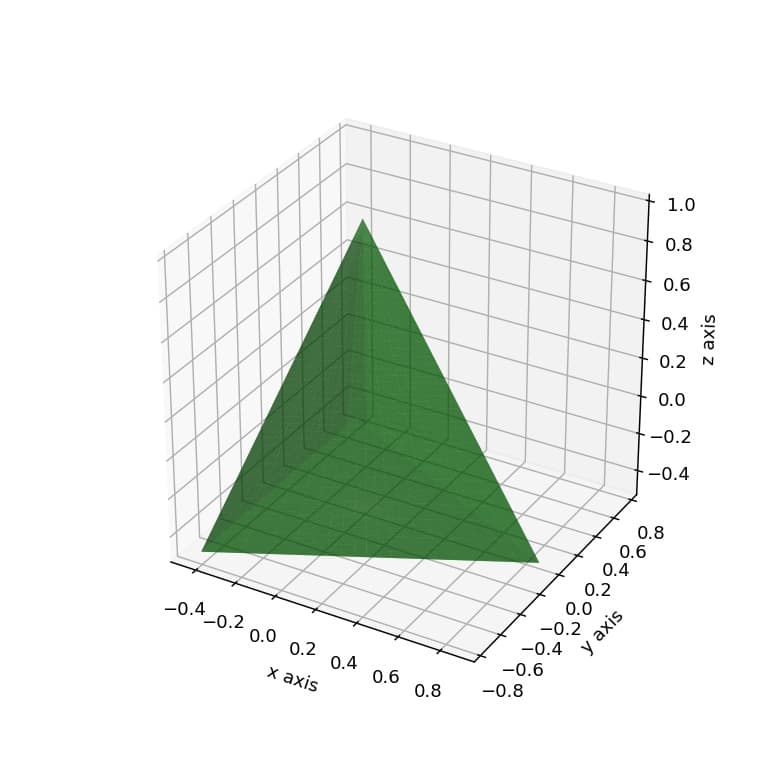
本記事では、matplotlibの3Dグラフ機能を使って正四面体（tetrahedron）を描画する方法を解説します。3次元空間での正四面体の作成方法から表示までを詳しく紹介していきます。
コード
解説
モジュールのインポート
バージョン
データの生成
2次元
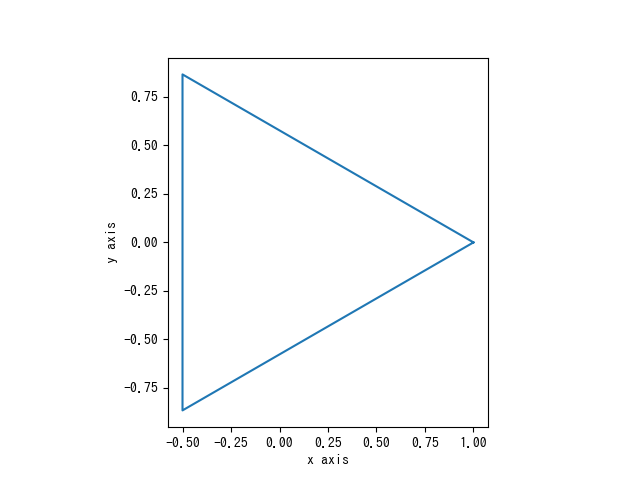
まずは2次元平面における正三角形について考えましょう。2次元での正三角形のコードと図は以下の通りです。
正n角形は、媒介変数tを0〜2πの範囲で考え、$$ a_n=\frac{2\pi}{n} $$とすると、
$$ x =\cos t \cdot \frac{\cos \frac{a_n}{2}}{\cos\left[a_n\left\{\frac{t}{a_n}-{\rm floor}\left(\frac{t}{a_n}\right)\right\}-\frac{a_n}{2}\right]}\\ y =\sin t \cdot \frac{\cos \frac{a_n}{2}}{\cos\left[a_n\left\{\frac{t}{a_n}-{\rm floor}\left(\frac{t}{a_n}\right)\right\}-\frac{a_n}{2}\right]} $$で表すことができます。この式は以下のサイトを参考にしました。
正多角形とスピログラフの数式
正多角形とスピログラフの数式です。 正多角形(2次元) 正多角形(3次元) 星型多角形(2次元) 星型多角形(…
slpr.sakura.ne.jp
3次元
2次元平面でxをpc(t)、yをps(t)と表すと、3次元空間におけるxyz座標は次のようになります。
$$ x = {\rm ps}(u)\cdot {\rm pc}(v) \\ y = {\rm ps}(u)\cdot {\rm ps}(v) \\ z = {\rm pc}(u) $$ここでは、媒介変数を$$0\le u \lt \pi, \;\; 0\le v \lt 2\pi$$の範囲で設定しています。
3Dグラフの設定
軸範囲、軸ラベルの設定
3Dグラフの表示
color=’g’を指定すると緑色に、alpha=0.5を設定すると半透明（透明度50%）の図形が描画されます。
回転アニメーション
作製した図を回転させると以下のようになります。
回転アニメーションは以下の記事を参考にして作成しました。
[matplotlib 3D] 14. 3Dグラフの回転アニメーション
matplotlib mplot3d のグラフの回転アニメーション
sabopy.com
2018.10.25
参考
三角錐 - Wikipedia
ja.wikipedia.org
正多角形とスピログラフの数式
正多角形とスピログラフの数式です。 正多角形(2次元) 正多角形(3次元) 星型多角形(2次元) 星型多角形(…
slpr.sakura.ne.jp
コメント