ローレンツアトラクタ
ローレンツアトラクタは、気象学者エドワード・ローレンツによって1963年に発見された決定論的カオスの代表的な例です。これは単純な非線形微分方程式系から生じる複雑な軌道を示し、初期条件への敏感な依存性(バタフライ効果)を表しています。ここでは、matplotlibのmplot3dによりローレンツアトラクタを3Dグラフ上に表示する方法を説明する。
コード
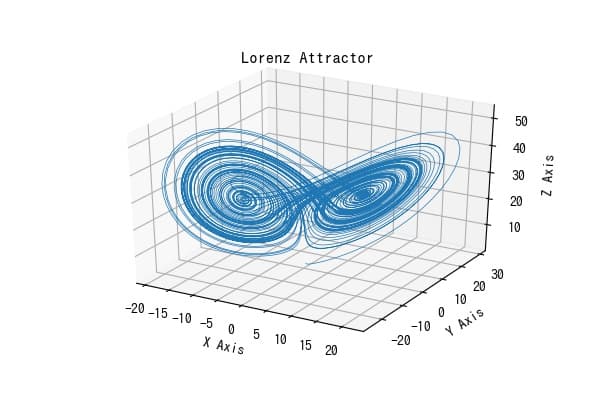
解説
ローレンツ・アトラクタとは
ローレンツ方程式は、カオス的挙動を示す非線形方程式です。この方程式には3つのパラメータ(σ, ρ, β)があり、これらが特定の値をとるときにローレンツアトラクタが生成されます。[1]
データの生成
def lorenz(x, y, z, s=10, r=28, b=2.667):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
ローレンツアトラクタは、特定のx、y、z座標に対応するx_dot、y_dot、z_dotの変化率を返す関数として定義されます。
xs = np.empty((num_steps + 1,))
np.emptyは初期化されていない配列を生成します。num_stepsが10000の場合、(10001,)の配列が作られます。np.emptyの主な特徴は、他の配列生成関数と比較して実行速度が速いことです。
xs[0], ys[0], zs[0] = (0., 1., 1.05)
各配列の0番目(1番最初)をそれぞれ設定します。
for i in range(num_steps):
x_dot, y_dot, z_dot = lorenz(xs[i], ys[i], zs[i])
xs[i + 1] = xs[i] + (x_dot * dt)
ys[i + 1] = ys[i] + (y_dot * dt)
zs[i + 1] = zs[i] + (z_dot * dt)
まず、計算の流れを考えてみましょう。i=0の初期状態では、初期値(xs[0], ys[0], zs[0])に対してlorenz関数を適用してxdotを求めます。次のステップxs[1]は、xs[0]に求めたx_dot×dt(=0.01)を加えた値になります。このプロセスをnum_steps(10000回)繰り返すことで、10000個のxs、ys、zsの値を算出します。
ローレンツ・アトラクタの表示
ax.plot(xs, ys, zs, lw=0.5)
lwは線の太さの設定となります。
ローレンツアトラクタをアニメーション表示
データポイント数を少なくしたローレンツアトラクタでアニメーションを表示します。
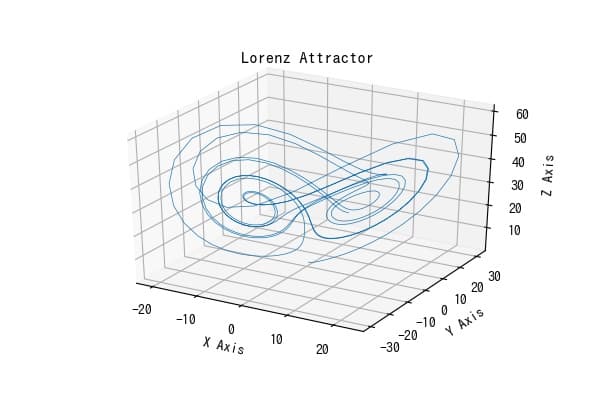
アニメーション
参考
https://ja.wikipedia.org/wiki/%E3%83%AD%E3%83%BC%E3%83%AC%E3%83%B3%E3%83%84%E6%96%B9%E7%A8%8B%E5%BC%8F
Lorenz attractor — Matplotlib 3.10.8 documentation

コメント